Derivation of Heron's / Hero's Formula for Area of Triangle

For a triangle of given three sides, say a, b, and c, the formula for the area is given by
 

 

where s is the semi perimeter equal to P/2 = (a + b + c)/2.
 

Derivation of Heron's Formula
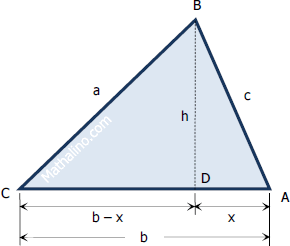Area of triangle ABC
$A = \frac{1}{2}bh$       → equation (1)
 

From triangle ADB
$x^2 + h^2 = c^2$

$x^2 = c^2 – h^2$

$x = \sqrt{c^2 - h^2}$
 

From triangle CDB
$(b – x)^2 + h^2 = a^2$

$(b – x)^2 = a^2 – h^2$

$b^2 – 2bx + x^2 = a^2 – h^2$
 

Substitute the values of x and x²
$b^2 – 2b\sqrt{c^2 - h^2} + (c^2 – h^2) = a^2 – h^2$

$b^2 + c^2 – a^2 = 2b\sqrt{c^2 - h^2}$
 

Square both sides
$(b^2 + c^2 – a^2)^2 = 4b^2(c^2 - h^2)$

$\dfrac{(b^2 + c^2 – a^2)^2}{4b^2} = c^2 - h^2$

$h^2 = c^2 - \dfrac{(b^2 + c^2 – a^2)^2}{4b^2}$

$h^2 = \dfrac{4b^2c^2 - (b^2 + c^2 – a^2)^2}{4b^2}$

$h^2 = \dfrac{(2bc)^2 - (b^2 + c^2 – a^2)^2}{4b^2}$

$h^2 = \dfrac{[ \, 2bc + (b^2 + c^2 – a^2) \, ][ \, 2bc - (b^2 + c^2 – a^2) \, ]}{4b^2}$

$h^2 = \dfrac{[ \, 2bc + b^2 + c^2 – a^2 \, ][ \, 2bc - b^2 - c^2 + a^2 \, ]}{4b^2}$

$h^2 = \dfrac{[ \, (b^2 + 2bc + c^2) – a^2 \, ][ \, a^2 - (b^2 - 2bc + c^2) \, ]}{4b^2}$

$h^2 = \dfrac{[ \, (b + c)^2 – a^2 \, ] \cdot [ \, a^2 - (b - c)^2 \, ]}{4b^2}$

$h^2 = \dfrac{[ \, (b + c) + a \, ][ \, (b + c) - a \, ] \cdot [ \, a + (b - c) \, ][ \, a - (b - c) \, ]}{4b^2}$

$h^2 = \dfrac{(b + c + a)(b + c - a)(a + b - c)(a - b + c)}{4b^2}$

$h^2 = \dfrac{(a + b + c)(b + c - a)(a + c - b)(a + b - c)}{4b^2}$

$h^2 = \dfrac{(a + b + c)(a + b + c - 2a)(a + b + c - 2b)(a + b + c - 2c)}{4b^2}$

$h^2 = \dfrac{P(P - 2a)(P - 2b)(P - 2c)}{4b^2}$   note: P = perimeter

$h = \dfrac{\sqrt{P(P - 2a)(P - 2b)(P - 2c)}}{2b}$
 

Substitute h to equation (1)
$A = \frac{1}{2}b\dfrac{\sqrt{P(P - 2a)(P - 2b)(P - 2c)}}{2b}$

$A = \frac{1}{4}\sqrt{P(P - 2a)(P - 2b)(P - 2c)}$

$A = \sqrt{\frac{1}{16}P(P - 2a)(P - 2b)(P - 2c)}$

$A = \sqrt{\dfrac{P}{2} \left( \dfrac{P - 2a}{2} \right)\left( \dfrac{P - 2b}{2} \right)\left( \dfrac{P - 2c}{2} \right)}$

$A = \sqrt{\dfrac{P}{2} \left( \dfrac{P}{2} - a \right)\left( \dfrac{P}{2} - b \right)\left( \dfrac{P}{2} - c \right)}$
 

Recall that P/2 = s. Thus,