Derivation of Formula for Area of Cyclic Quadrilateral

For a cyclic quadrilateral with given sides a, b, c, and d, the formula for the area is given by
 

 

Where s = (a + b + c + d)/2 known as the semi-perimeter.
 

Derivation of Formula
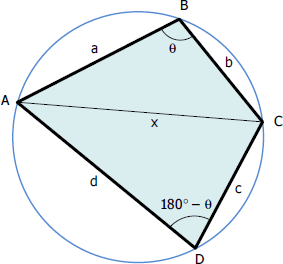Cosine law for triangle ABC
$x^2 = a^2 + b^2 – 2ab \cos \theta$
 

Cosine law for triangle ADC

$x^2 = c^2 + d^2 – 2cd \cos (180^\circ – \theta)$

note that cos (180° - x) = -cos x
$x^2 = c^2 + d^2 + 2cd \cos \theta$
 

Equate the two x²

$x^2 = x^2$

$a^2 + b^2 – 2ab \cos \theta = c^2 + d^2 + 2cd \cos \theta$

$a^2 + b^2 – c^2 - d^2 = 2ab \cos \theta + 2cd \cos \theta$

$a^2 + b^2 – c^2 - d^2 = 2(ab + cd) \cos \theta$

$\cos \theta = \dfrac{a^2 + b^2 – c^2 - d^2}{2(ab + cd)}$
 

Area of ABCD

$A = A_{ABC} + A_{ADC}$

$A = \frac{1}{2}ab \sin \theta + \frac{1}{2}cd \sin (180^\circ – \theta)$   ←   note that sin (180° - θ) = sin θ

$A = \frac{1}{2}ab \sin \theta + \frac{1}{2}cd \sin \theta$

$A = \frac{1}{2}(ab + cd) \sin \theta$
 

Square both sides of the equation

$A^2 = \frac{1}{4}(ab + cd)^2 \sin^2 \theta$

$A^2 = \frac{1}{4}(ab + cd)^2 (1 - \cos^2 \theta)$
 

From

$\cos \theta = \dfrac{a^2 + b^2 – c^2 - d^2}{2(ab + cd)}$

$\cos^2 \theta = \dfrac{(a^2 + b^2 – c^2 - d^2)^2}{4(ab + cd)^2}$

$1 - \cos^2 \theta = 1 - \dfrac{(a^2 + b^2 – c^2 - d^2)^2}{4(ab + cd)^2}$

$1 - \cos^2 \theta = \dfrac{4(ab + cd)^2 - (a^2 + b^2 – c^2 - d^2)^2}{4(ab + cd)^2}$

$1 - \cos^2 \theta = \dfrac{4(ab + cd)^2 - (a^2 + b^2 – c^2 - d^2)^2}{4(ab + cd)^2}$

$1 - \cos^2 \theta = \dfrac{[ \, 2(ab + cd) + (a^2 + b^2 – c^2 - d^2) \, ][ \, 2(ab + cd) - (a^2 + b^2 – c^2 - d^2) \, ]}{4(ab + cd)^2}$

$1 - \cos^2 \theta = \dfrac{[ \, 2ab + 2cd + a^2 + b^2 – c^2 - d^2 \, ][ \, 2ab + 2cd - a^2 - b^2 + c^2 + d^2 \, ]}{4(ab + cd)^2}$

$1 - \cos^2 \theta = \dfrac{[ \, (a^2 + 2ab + b^2) – (c^2 - 2cd + d^2) \, ][ \, (c^2 + 2cd + d^2) - (a^2 - 2ab + b^2) \, ]}{4(ab + cd)^2}$

$1 - \cos^2 \theta = \dfrac{[ \, (a + b)^2 – (c - d)^2 \, ][ \, (c + d)^2 - (a - b)^2 \, ]}{4(ab + cd)^2}$

$1 - \cos^2 \theta = \dfrac{[ \, (a + b) + (c - d) \, ][ \, (a + b) – (c - d) \, ][ \, (c + d) + (a - b) \, ][ \, (c + d) - (a - b) \, ]}{4(ab + cd)^2}$

$1 - \cos^2 \theta = \dfrac{(a + b + c - d)(a + b + d – c)(a + c + d - b)(b + c + d - a)}{4(ab + cd)^2}$

$1 - \cos^2 \theta = \dfrac{(b + c + d - a)(a + c + d - b)(a + b + d – c)(a + b + c - d)}{4(ab + cd)^2}$

$1 - \cos^2 \theta = \dfrac{(a + b + c + d - 2a)(a + b + c + d - 2b)(a + b + c + d – 2c)(a + b + c + d - 2d)}{4(ab + cd)^2}$
 

Note that a + b + c + d = P, the perimeter. Thus,

$1 - \cos^2 \theta = \dfrac{(P - 2a)(P - 2b)(P – 2c)(P - 2d)}{4(ab + cd)^2}$
 

Substitute 1 - cos² θ to the equation of A² above.

$A^2 = \frac{1}{4}(ab + cd)^2 \left[ \dfrac{(P - 2a)(P - 2b)(P – 2c)(P - 2d)}{4(ab + cd)^2} \right]$

$A^2 = \frac{1}{16}(P - 2a)(P - 2b)(P – 2c)(P - 2d)$

$A^2 = \left( \dfrac{P - 2a}{2} \right)\left( \dfrac{P - 2b}{2} \right)\left( \dfrac{P - 2c}{2} \right)\left( \dfrac{P - 2d}{2} \right)$

$A^2 = (\frac{1}{2}P - a)(\frac{1}{2}P - b)(\frac{1}{2}P – c)(\frac{1}{2}P - d)$
 

Recall that   $\frac{1}{2}P = \frac{1}{2}(a + b + c + d) = s$, the semi-perimeter. Thus,

$A^2 = (s - a)(s - b)(s – c)(s - d)$
 

Finally,