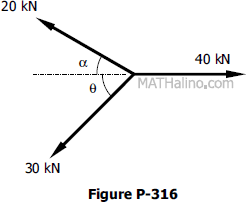
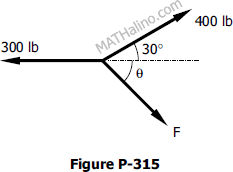
Solving for angle $A$ in triangle ABC
Problem 10
In a triangle ABC, if $\dfrac{2 \cos A}{a} + \dfrac{\cos B}{b} + \dfrac{2 \cos C}{c} = \dfrac{a}{bc} + \dfrac{b}{ca}$, find the value of angle $A$.
- Read more about Solving for angle $A$ in triangle ABC
- Log in to post comments