The Cyclic Quadrilateral
A quadrilateral is said to be cyclic if its vertices all lie on a circle. In cyclic quadrilateral, the sum of two opposite angles is 180° (or π radian); in other words, the two opposite angles are supplementary.
$A + C = 180^\circ$
$B + D = 180^\circ$
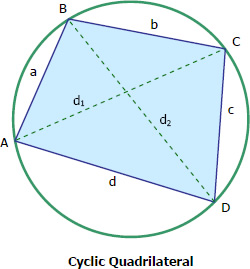
The area of cyclic quadrilateral is given by
$A = \sqrt{(s - a)(s - b)(s - c)(s - d)}$
See the derivation of area of cyclic quadrilateral for profound details.
Ptolemy's Theorem for Cyclic Quadrilateral
For any cyclic quadrilateral, the product of the diagonals is equal to the sum of the products of non-adjacent sides. In other words
$d_1 d_2 = ac + bd$
See the proof of Ptolemy's theorem for cyclic quadrilateral.
