The Polygon
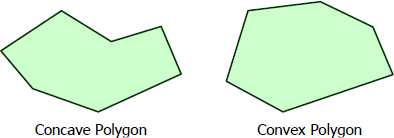
Polygon is a closed plane figure bounded by straight lines. There are two basic types of polygons, a convex and a concave polygon. Polygon is said to be convex if no side when extended will pass inside the polygon, otherwise it is concave.
Name of Polygons
| No. of Sides, n | Name |
| 1 | Monogon, Henagon (cannot exist) |
| 2 | Digon (cannot exist) |
| 3 | Triangle, Trigon |
| 4 | Quadrilateral, Quadrangle, Tetragon |
| 5 | Pentagon |
| 6 | Hexagon |
| 7 | Heptagon, Septagon |
| 8 | Octagon |
| 9 | Nonagon, Enneagon |
| 10 | Decagon |
| 11 | Undecagon, Hendecagon |
| 12 | Dodecagon, Duodecagon |
| 13 | Tridecagon, Triskaidecagon |
| 14 | Tetradecagon, Tetrakaidecagon |
| 15 | Pentadecagon, Quindecagon, Pentakaidecagon |
| 16 | Hexadecagon, Hexakaidecagon |
| 17 | Heptadecagon, Heptakaidecagon |
| 18 | Octadecagon, Octakaidecagon |
| 19 | Enneadecagon, Ennekaidecagon, Nonadecagon |
| 20 | Icosagon |
| 30 | Triacontagon |
| 40 | Tetracontagon |
| 50 | Pentacontagon |
| 70 | Heptacontagon |
| 80 | Octacontagon |
| 90 | Enneacontagon |
| 100 | Hectogon |
| 1000 | Chilliagon |
| 10 000 | Myriagon |
| 1 000 000 | Megagon |
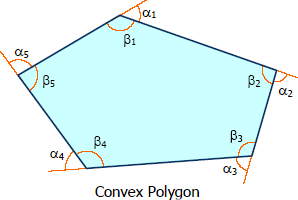
The following are true for convex polygon
- The sum of the angles of polygon of n sides is 180°(n - 2) right angles.
- The exterior angles of a polygon are together equal to 4 right angles.
Formulas for convex polygon
$\Sigma \beta = 180^\circ (n - 2)$
$\Sigma \alpha = 360^\circ$
$D = \dfrac{n}{2}(n - 3)$
- Log in to post comments
