Quadrilateral Circumscribing a Circle

Tags:

Quadrilateral circumscribing a circle (also called tangential quadrilateral) is a quadrangle whose sides are tangent to a circle inside it.

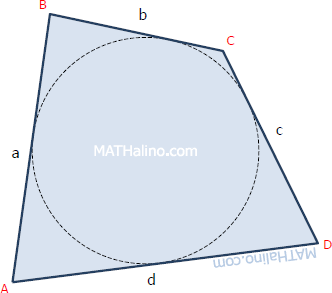
Area,

$A = rs$

Where r = radius of inscribed circle and s = semi-perimeter = (a + b + c + d)/2

Derivation for area
Let O and r be the center and radius of the inscribed circle, respectively.

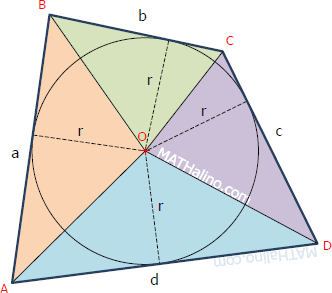
$A_{AOB} = \frac{1}{2}ar$

$A_{BOC} = \frac{1}{2}br$

$A_{COD} = \frac{1}{2}cr$

$A_{AOD} = \frac{1}{2}dr$

Total area
$A = A_{AOB} + A_{BOC} + A_{COD} + A_{AOD}$

$A = \frac{1}{2}ar + \frac{1}{2}br + \frac{1}{2}cr + \frac{1}{2}dr$

$A = \frac{1}{2}(a + b + c + d)r$

$A = sr$ (okay!)

Some known properties

Opposite sides subtend supplementary angles at the center of inscribed circle. From the figure above, ∠AOB + ∠COD = 180° and ∠AOD + ∠BOC = 180°.
The area can be divided into four kites. See figure below.
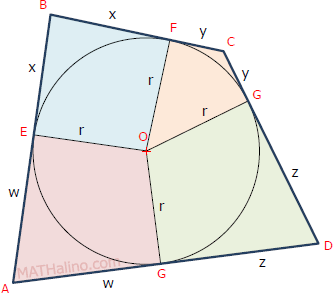
If the opposite angles are equal (A = C and B = D), it is a rhombus.

Submitted by Romel Verterra on June 3, 2012 - 9:12am

MATHalino.com