The Triangle
Definition of a Triangle
Triangle is a closed figure bounded by three straight lines called sides. It can also be defined as polygon of three sides.
Area of triangle
The area of the triangle is given by the following formulas:
$A = \frac{1}{2}bh$
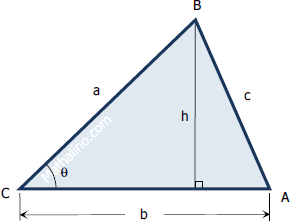
Given two sides and included angle
$A = \frac{1}{2}ab \sin \theta$
Given three sides (see the derivation of Hero's formula)
$A = \sqrt{s(s - a)(s - b)(s - c)}$
where, $s = \frac{1}{2}(a + b + c)$ called the semi-perimeter.
Given one side and three angles (say angles A, B, and C, and side b are given)
$Area = \dfrac{b^2\sin A~\sin C}{2\sin B}$
See also the links below:
