Common Quadrilaterals

Tags:

Square

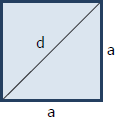
Area, $A = a^2$

Perimeter, $P = 4a$

Diagonal, $d = a\sqrt{2}$

Rectangle

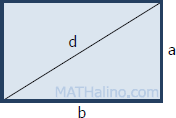
Area, $A = ab$

Perimeter, $P = 2(a + b)$

Diagonal, $d = \sqrt{a^2 + b^2}$

Rhombus

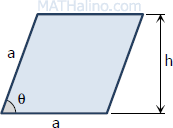
Area, $A = a^2 \sin \theta = ah$

Perimeter, $P = 4a$

Shorter diagonal, $d_1 = a\sqrt{2 - 2 \cos \theta}$

longer diagonal, $d_2 = a\sqrt{2 + 2 \cos \theta}$

Note: The diagonals of square and rhombus are perpendicular to each other.

Parallelogram

Area, $A = ab \sin \theta = ah$

Perimeter, $P = 2(a + b)$

Shorter diagonal, $d_1 = \sqrt{a^2 + b^2 - 2ab \cos \theta}$

Longer diagonal, $d_2 = \sqrt{a^2 + b^2 + 2ab \cos \theta}$

Trapezoid

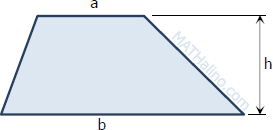
Area, $A = \frac{1}{2}(a + b)h$

Submitted by Romel Verterra on June 2, 2012 - 10:34pm

Recent Updates