Trapezoid
02 Trapezoidal lot segregated from triangular land
Situation
A triangular lot ABC have side BC = 400 m and angle B = 50°. The lot is to be segregated by a dividing line DE parallel to BC and 150 m long. The area of segment BCDE is 50,977.4 m2.
Part 1: Calculate the area of lot ABC.
A. 62,365 m2
B. 59,319 m2
C. 57,254 m2
D. 76.325 m2
Part 2: Calculate the area of lot ADE.
A. 8,342 m2
B. 14,475 m2
C. 6,569 m2
D. 11,546 m2
Part 3: Calculate the value of angle C
A. 57°
B. 42°
C. 63°
D. 68°
Length of one side for maximum area of trapezoid (solution by Geometry)
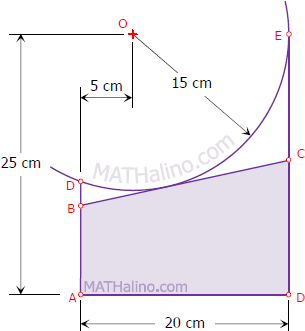
Problem
BC of trapezoid ABCD is tangent at any point on circular arc DE whose center is O. Find the length of BC so that the area of ABCD is maximum.
Common Quadrilaterals
Square
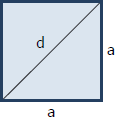
Perimeter, $P = 4a$
Diagonal, $d = a\sqrt{2}$
- Read more about Common Quadrilaterals
- Log in to post comments
Trapezoidal Strip of Land from a Triangular Lot
Problem
A strip of 640 m2 is sold from a triangular field whose sides are 96 m, 72 m, and 80 m. The strip is of uniform width h and has one of its sides parallel to the longest side of the field. Find the width of the strip.
A. 7.1 m
B. 8.1 m
C. 8.7 m
D. 7.7 m
41 - 42 Maxima and Minima Problems Involving Trapezoidal Gutter
Problem 41
In Problem 39, if the strip is L in. wide, and the width across the top is T in. (T < L), what base width gives the maximum capacity?
38 - 40 Solved problems in maxima and minima
Problem 38
A cylindrical glass jar has a plastic top. If the plastic is half as expensive as glass, per unit area, find the most economical proportion of the jar.
- Read more about 38 - 40 Solved problems in maxima and minima
- Log in to post comments