Trapezoidal Strip of Land from a Triangular Lot

From ΔABC (By cosine law:)
$80^2 = 72^2 + 96^2 - 2(72)(96) \cos \alpha$

$\alpha = 54.64^\circ$
 

$72^2 = 80^2 + 96^2 - 2(80)(96) \cos \beta$

$\beta = 47.22^\circ$
 

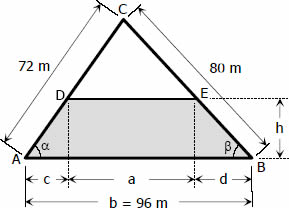$\tan \alpha = \dfrac{h}{c}$

$c = \dfrac{h}{\tan 54.64^\circ}$

$c = 0.7096h$
 

$\tan \beta = \dfrac{h}{c}$

$c = \dfrac{h}{\tan 47.22^\circ}$

$c = 0.9254h$
 

$a = b - c - d$

$a = 96 - 0.7096h - 0.9254h$

$a = 96 - 1.635h$
 

$A_{ABED} = \frac{1}{2}(a + b)h$

$640 = \frac{1}{2} [ \, (96 - 1.635h) + 96 \, ] \, h$

$1280 = 192h - 1.635h^2$

$1.635h^2 - 192h + 1280 = 0$

$h = 110.34 \, \text{ and } \, 7.09$
 

use h = 7.09 m.           (answer: A)