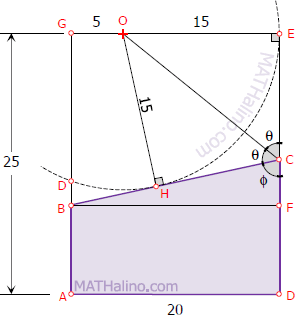
Let
$\theta$ = ∠HCO = ∠ECO
$\varphi = 180^\circ - 2\theta$
From right triangle BFC
$\tan \varphi = \dfrac{20}{CF}$
$CF = \dfrac{20}{\tan \varphi} = \dfrac{20}{\tan (180^\circ - 2\theta)}$
$CF = -\dfrac{20}{\tan 2\theta}$
From right triangle CEO
$\tan \theta = \dfrac{15}{CE}$
$CE = \dfrac{15}{\tan \theta}$
$BG = CE + CF$
$BG = \dfrac{15}{\tan \theta} - \dfrac{20}{\tan 2\theta}$
Area of trapezoid BCEG
$A_{BCEG} = \frac{1}{2}(CE + BG)(20)$
$A_{BCEG} = 10 \left[ \dfrac{15}{\tan \theta} + \left( \dfrac{15}{\tan \theta} - \dfrac{20}{\tan 2\theta} \right) \right]$
$A_{BCEG} = \dfrac{300}{\tan \theta} - \dfrac{200}{\tan 2\theta}$
Area of trapezoid ABCD
$A = A_{ADEG} - A_{BCEG}$
$A = 25(20) - \left( \dfrac{300}{\tan \theta} - \dfrac{200}{\tan 2\theta} \right)$
$A = 500 - 300 \cot \theta + 200 \cot 2\theta$
For maximum area, dA/dθ = 0:
$\dfrac{dA}{d\theta} = -300(-\csc^2 \theta) + 200 (-2 \csc^2 2\theta) = 0$
$300\csc^2 \theta - 400 \csc^2 2\theta = 0$
$3\csc^2 \theta = 4 \csc^2 2\theta$
$\sqrt{3} \csc \theta = 2 \csc 2\theta$
$\dfrac{\sqrt{3}}{\sin \theta} = \dfrac{2}{\sin 2\theta}$
$\dfrac{\sqrt{3}}{\sin \theta} = \dfrac{2}{2\sin \theta \cos \theta}$
$\cos \theta = \dfrac{1}{\sqrt{3}}$
$\theta = 54.74^\circ$
$\varphi = 180^\circ - 2\theta = 180^\circ - 2(54.74^\circ)$
$\varphi = 70.53^\circ$
From right triangle BFC
$\sin \varphi = \dfrac{20}{BC}$
$BC = \dfrac{20}{\sin \varphi} = \dfrac{20}{\sin 70.53^\circ}$
$BC = 21.21 \, \text{ cm}$ answer
A solution to the same problem has been done by Geometry without the use of Calculus. In that solution, the location of the tangent point H has been pointed out by direct analogy. See how it was done by following this link: Solution by Geometry alone
