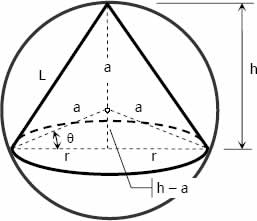
$r = a \cos \theta$
$h = a \sin \theta + a = a(\sin \theta + 1)$
$L = \sqrt{h^2 + r^2}$
$L = \sqrt{[\, a(\sin \theta + 1) \, ]^2 + (a \cos \theta)^2}$
$L = \sqrt{a^2(\sin \theta + 1)^2 + a^2 \cos^2 \theta}$
$L = a\sqrt{(\sin \theta + 1)^2 + \cos^2 \theta}$
$L = a\sqrt{(\sin^2 \theta + 2\sin \theta + 1) + \cos^2 \theta}$
$L = a\sqrt{(\sin^2 \theta + 2\sin \theta + 1) + \cos^2 \theta}$
$L = a\sqrt{2\sin \theta + 1 + (\sin^2 \theta + \cos^2 \theta)}$
$L = a\sqrt{2\sin \theta + 1 + 1}$
$L = a\sqrt{2\sin \theta + 2}$
Convex area of cone:
$A_L = \pi rL$
$A_L = \pi (a \cos \theta)\left(a\sqrt{2\sin \theta + 2}\right)$
$A_L = \pi a^2 \cos \theta \sqrt{2\sin \theta + 2}$
$\dfrac{dA_L}{d\theta} = \pi a^2 \left( \cos \theta \dfrac{2\cos \theta}{2\sqrt{2\sin \theta + 2}} - \sin \theta \sqrt{2\sin \theta + 2} \right) = 0$
$\dfrac{\cos^2 \theta}{\sqrt{2\sin \theta + 2}} = \sin \theta \sqrt{2\sin \theta + 2}$
$\cos^2 \theta = \sin \theta (2\sin \theta + 2)$
$1 - \sin^2 \theta = 2\sin^2 \theta + 2\sin \theta$
$3\sin^2 \theta + 2\sin \theta - 1 = 0$
$(3\sin \theta - 1)(\sin \theta + 1) = 0$
for
$3\sin \theta - 1 = 0$
$\sin \theta = 1/3$
for
$\sin \theta + 1 = 0$
$\sin \theta = - 1$ → (meaningless)
use
$\sin \theta = 1/3$
$h = a(\sin \theta + 1)$
$h = a(\frac{1}{3} + 1)$
$h = \frac{4}{3} \, a$ answer
