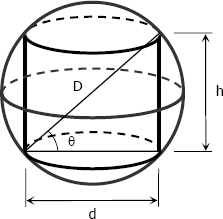
A shot is in the form of a sphere and the cylinder is the cylinder of maximum. From the figure )This is also the
figure used in Solution 02:
$V_c = \frac{1}{4}\pi d^2h$
Where:
$d = D \cos \theta$
$h = D \sin \theta$
Thus,
$V_c = \frac{1}{4}\pi (D\cos \theta)^2(\sin \theta)$
$V_c = \frac{1}{4}D^3\pi \cos^2 \theta \sin \theta$
$\dfrac{dV_c}{d\theta} = \frac{1}{4}D^3\pi [ \, \cos^2 \theta (\cos \theta) + \sin \theta (-2\cos \theta \sin \theta) \, ]$
$\dfrac{dV_c}{d\theta} = \frac{1}{4}D^3\pi (\cos^3 \theta - 2\sin^2 \theta \cos \theta) = 0$
$2\sin^2 \theta \cos \theta = \cos^3 \theta$
$2\sin^2 \theta = \cos^2 \theta$
$\dfrac{\sin^2 \theta}{\cos^2 \theta} = \dfrac{1}{2}$
$\tan^2 \theta = \frac{1}{2}$
$\tan \theta = \frac{1}{\sqrt{2}}$
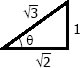$\cos \theta = \frac{\sqrt{2}}{\sqrt{3}}$
$\sin \theta = \frac{1}{\sqrt{3}}$
$V_c = \frac{1}{4}D^3\pi \left(\frac{\sqrt{2}}{\sqrt{3}}\right)^2 \left(\frac{1}{\sqrt{3}}\right)$
$V_c = \frac{1}{6\sqrt{3}}\pi D^3$ → Maximum volume of cylinder
Volume of shot (sphere):
$V_s = \frac{4}{3}\pi R^3 = \frac{4}{3}\pi (D/2)^3$
$V_s = \frac{1}{6}\pi D^3$
Weight is proportional to the volume, so
$\dfrac{W_c}{V_c} = \dfrac{W_s}{V_s}$
$W_c = \dfrac{W_s}{V_s} \, \times \, V_c$
$W_c = \dfrac{16}{\frac{1}{6}\pi D^3} \, \times \, \frac{1}{6\sqrt{3}}\pi D^3$
$W_c = 9.24 \, \text{ lb}$ answer
