22 - Smallest cone that may circumscribe a sphere

Volume of cone:
$V = \frac{1}{3} \pi r^2 h$
 

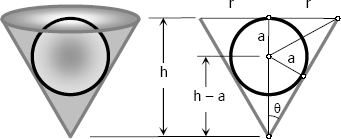From the figure:
$\csc \theta = \dfrac{h - a}{a}$

$h = a \csc \theta + a$

$h = a(\csc \theta + 1)$
 

$\tan \theta = \dfrac{r}{h}$

$r = h \tan \theta$

$r = a(\csc \theta + 1) \tan \theta$
 

$V = \frac{1}{3} \pi [\,a(\csc \theta + 1) \tan \theta \,]^2 [\, a(\csc \theta + 1) \,]$

$V = \frac{1}{3} \pi a^3(\csc \theta + 1)^3 \tan^2 \theta$

$\dfrac{dV}{d\theta} = \frac{1}{3} \pi a^3 \left[ (\csc \theta + 1)^3 (2\tan \theta \sec^2 \theta) + 3\tan^2 \theta (\csc \theta + 1)^2 (-\csc \theta \cot \theta) \right] = 0$

$2\tan \theta \sec^2 \theta(\csc \theta + 1)^3 - 3\tan^2 \theta \csc \theta \cot \theta (\csc \theta + 1)^2 = 0$

$2 \sec^2 \theta(\csc \theta + 1) - 3\tan \theta \csc \theta \cot \theta = 0$

$2 \left( \dfrac{1}{\cos^2 \theta} \right) \left( \dfrac{1}{\sin \theta} + 1 \right) - 3\tan \theta \left( \dfrac{1}{\sin \theta} \right) \left( \dfrac{1}{\tan \theta} \right) = 0$

$2 \left( \dfrac{1}{\cos^2 \theta} \right) \left( \dfrac{1}{\sin \theta} + 1 \right) = 3\left( \dfrac{1}{\sin \theta} \right)$

$2 \sin \theta \left( \dfrac{1}{\sin \theta} + 1 \right) = 3\cos^2 \theta$

$2 + 2\sin \theta = 3 \cos^2 \theta$

$2 + 2\sin \theta = 3(1 - \sin^2 \theta)$

$3\sin^2 \theta + 2\sin \theta - 1 = 0$

$(3\sin \theta - 1)(\sin \theta + 1) = 0$
 

for
$3 \sin \theta - 1 = 0$

$\sin \theta = 1/3$
 

for
$\sin \theta + 1 = 0$

$\sin \theta = -1$   ←   (meaningless)
 

use
$\sin \theta = 1/3$
 

$h = a(\csc \theta + 1)$

$h = a \left( \dfrac{1}{\sin \theta} + 1 \right)$

$h = a \left( \dfrac{1}{1/3} + 1 \right)$

$h = 4a$           answer