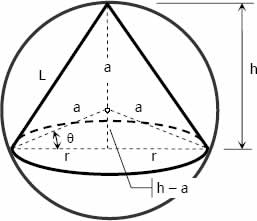
Volume of cone
$V_c = \frac{1}{3}\pi r^2 h$
Where:
$r = a \cos \theta$
$h = a \sin \theta + a = a(\sin \theta + 1)$
$V_c = \frac{1}{3}\pi (a \cos \theta)^2 [\, a (\sin \theta + 1) \,]$
$V_c = \frac{1}{3}\pi a^3 \cos^2 \theta (\sin \theta + 1)$
$\dfrac{dV_c}{d\theta} = \frac{1}{3}\pi a^3 \Big\{ \cos^2 \theta (\cos \theta) + (\sin \theta + 1)[\,2\cos \theta(-\sin \theta)\,] \Big\} = 0$
$\cos^3 \theta - 2\sin \theta \cos \theta (\sin \theta + 1) = 0$
$\cos^2 \theta - 2\sin \theta (\sin \theta + 1) = 0$
$(1 - \sin^2 \theta) - 2\sin^2 \theta - 2\sin \theta = 0$
$1 - 3\sin^2 \theta - 2\sin \theta = 0$
$3\sin^2 \theta + 2\sin \theta - 1 = 0$
$(3\sin \theta - 1)(\sin \theta + 1) = 0$
for
$3\sin \theta - 1 = 0$
$\sin \theta = 1/3$
for
$\sin \theta + 1 = 0$
$\sin \theta = -1$ → (meaningless)
use
$\sin \theta = 1/3$
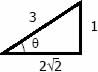$V_c = \frac{1}{3}\pi a^3 \left( \dfrac{2\sqrt{2}}{3} \right)^2 (\frac{1}{3} + 1)$
$V_c = \frac{32}{81}\pi a^3$
Volume of sphere:
$V_s = \frac{4}{3}\pi a^3$
$\text{Material saved } = \dfrac{V_c}{V_s} \times 100\%$
$\text{Material saved } = \dfrac{\frac{32}{81}\pi a^3}{\frac{4}{3}\pi a^3} \times 100\%$
$\text{Material saved} = 29.63\% ~ (\text{about } 30\%)$ answer
