17-18 A man in a motorboat needs to catch a bus

$x = 30 \tan \theta$

$s = 30 \sec \theta$
 

$\text{Time}_{\text{boat}} = \text{Time}_{\text{bus}} + 1$
 

Note: time = distance / rate
Let r = rate of boat

 

Thus,
$\dfrac{s}{r} = \dfrac{x}{40} + 1$

$\dfrac{30 \sec \theta}{r} = \dfrac{30 \tan \theta}{40} + 1$

$\dfrac{30 \sec \theta}{r} = \dfrac{3 \tan \theta}{4} + 1$

$\dfrac{30 \sec \theta}{r} = \dfrac{3 \tan \theta + 4}{4}$

$r = \dfrac{120\sec \theta}{3\tan \theta + 4}$

$\dfrac{dr}{d\theta} = \dfrac{(3\tan \theta + 4)(120\sec \theta \tan \theta) - 120\sec \theta (3\sec^2 \theta)}{(3\tan \theta + 4)^2} = 0$

$120\sec \theta \tan \theta(3\tan \theta + 4) - 360\sec^3 \theta = 0$

$\tan \theta(3\tan \theta + 4) - 3\sec^2 \theta = 0$

$3\tan^2 \theta + 4\tan \theta - 3(1 + \tan^2 \theta) = 0$

$3\tan^2 \theta + 4\tan \theta - 3 - 3\tan^2 \theta = 0$

$4\tan \theta - 3 = 0$

$\tan \theta = 3/4$
 

$r = \dfrac{120\sec \theta}{3\tan \theta + 4}$

$r = \dfrac{120(5/4)}{3(3/4) + 4}$

$r = 24 \, \text{ miles per hour}$           answer

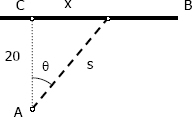
$x = 20 \tan \theta$

$s = 20 \sec \theta$
 

$\text{Time}_{\text{boat}} = \text{Time}_{\text{bus}} + \frac{18}{60}$
 

Note: time = distance / rate
Let r = rate of boat

 

Thus,
$\dfrac{s}{r} = \dfrac{x}{50} + \dfrac{18}{60}$

$\dfrac{20 \sec \theta}{r} = \dfrac{20 \tan \theta}{50} + \dfrac{3}{10}$

$1000 \sec \theta = 20r \tan \theta + 15r$

$200 \sec \theta = (4 \tan \theta + 3)r$

$r = \dfrac{200 \sec \theta}{4 \tan \theta + 3}$

$\dfrac{dr}{d\theta} = \dfrac{(4 \tan \theta + 3)(200 \sec \theta \, \tan \theta) - 200 \sec \theta (4 \sec^2 \theta)}{(4 \tan \theta + 3)^2} = 0$

$\dfrac{200 \sec \theta \, \tan \theta\,(4 \tan \theta + 3) - 800 \sec^3 \theta}{(4 \tan \theta + 3)^2} = 0$

$200 \sec \theta \, \tan \theta\,(4 \tan \theta + 3) - 800 \sec^3 \theta = 0$

$\tan \theta\,(4 \tan \theta + 3) - 4 \sec^2 \theta = 0$

$4 \tan^2 \theta + 3\tan \theta - 4 (1 + \tan^2 \theta) = 0$

$4 \tan^2 \theta + 3\tan \theta - 4 - 4\tan^2 \theta = 0$

$3\tan \theta - 4 = 0$

$\tan \theta = 4/3$
 

$r = \dfrac{200 \sec \theta}{4 \tan \theta + 3}$

$r = \dfrac{200 (5/3)}{4(4/3) + 3}$

$r = 40 \, \text{ miles per hour}$           answer