Sphere
Problem
A meteorologist is inflating a spherical balloon with a helium gas. If the radius of a balloon is changing at a rate of 1.5 cm/sec., express the volume V of the balloon as a function of time t (in seconds). Hint: Use composite function relationship Vsphere = 4/3 πr3 as a function of x (radius), and x (radius) as a function of t (time).
| A. V(t) = 5/2 πt3 | C. V(t) = 9/2 πt3 |
| B. V(t) = 7/2 πt3 | D. V(t) = 3/2 πt3 |
034 Review Problem - Sphere dropped into a cone
The inside of a vase is an inverted cone 2.983 in. across the top and 5.016 in. deep. If a heavy sphere 2.498 in. in diameter is dropped into it when the vase is full of water, how much water will overflow?
- Read more about 034 Review Problem - Sphere dropped into a cone
- Log in or register to post comments
033 Review Problem - Finding which one is the better bargain
Problem 33
Disregarding quality, and considering oranges as spheres, determine which is the better bargain, oranges 2-3/4 in. in diameter at 15 cents per dozen, or oranges averaging 3-1/2 in. in diameter at 30 cents per dozen.
015 Review Problem - Volume of spherical shell
Problem 15
A spherical shell 2 in. thick has an outer diameter of 12 in. Find the volume of the material of which it is made.
- Read more about 015 Review Problem - Volume of spherical shell
- Log in or register to post comments
003 Review Problem - Sphere melted into cylinder
Problem 3
Two spheres of lead, of radii 2 and 3 in., respectively, are melted into a cylinder of revolution of radius 1 in. Find the altitude of the cylinder.
- Read more about 003 Review Problem - Sphere melted into cylinder
- Log in or register to post comments
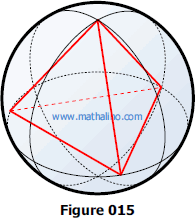
016 Radius of the sphere circumscribing a regular triangular pyramid
Example 016
Find the area of the surface and the volume of the sphere circumscribed about a regular tetrahedron of edge 25 cm. See Figure 015.
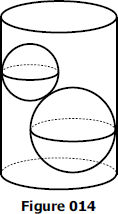
015 Two unequal balls inside the cylinder
Example 015
Two balls, one 15 cm in diameter and the other 10 cm in diameter, are placed in a cylindrical jar 20 cm in diameter, as shown in Figure 014. Find the volume of water necessary to cover them.
- Read more about 015 Two unequal balls inside the cylinder
- Log in or register to post comments
013 Insciribed and circumscribed sphere about a cube - volume comparison
Example 013
Compare the volume of a sphere inscribed in a cube with volume of the sphere that circumscribes the cube.