perimeter

Problem
What is the perimeter of the curve r = 4(1 + sin θ)?
 

The answer is 32 units. For detailed solution, follow the link by clicking on the figure.
 

Situation
A swimming pool is shaped from two intersecting circles 9 m in radius with their centers 9 m apart.
 

Part 1: What is the area common to the two circles?
A. 85.2 m²
B. 63.7 m²
C. 128.7 m²
D. 99.5 m²
 

Part 2: What is the total water surface area?
A. 409.4 m²
B. 524.3 m²
C. 387.3 m²
D. 427.5 m²
 

Part 3: What is the perimeter of the pool, in meters?
A. 63.5 m
B. 75.4 m
C. 82.4 m
D. 96.3 m
 

Square

 

 

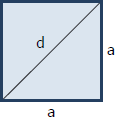
Area, $A = a^2$

Perimeter, $P = 4a$

Diagonal, $d = a\sqrt{2}$