rectangle

Square

 

 

Area, $A = a^2$

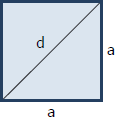
Perimeter, $P = 4a$

Diagonal, $d = a\sqrt{2}$

Problem 01
Find the shape of the rectangle of maximum perimeter inscribed in a circle.
 

Quadrilateral is a polygon of four sides and four vertices. It is also called tetragon and quadrangle. In the triangle, the sum of the interior angles is 180°; for quadrilaterals the sum of the interior angles is always equal to 360°
 

Classifications of Quadrilaterals
There are two broad classifications of quadrilaterals; simple and complex. The sides of simple quadrilaterals do not cross each other while two sides of complex quadrilaterals cross each other.
 

Simple quadrilaterals are further classified into two: convex and concave. Convex if none of the sides pass through the quadrilateral when prolonged while concave if the prolongation of any one side will pass inside the quadrilateral.
 

Problem 21
Find the rectangle of maximum perimeter inscribed in a given circle.