Quadrilateral with one side as diameter of circumscribing circle

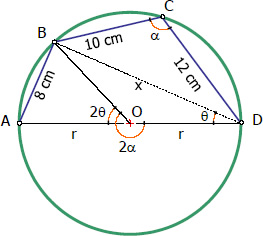From the figure:
$2\alpha = 2\theta + 180^\circ$

$\alpha = \theta + 90^\circ$
 

From triangle BCD (Using Cosine Law):

$x^2 = 10^2 + 12^2 - 2(10)(12)\cos \alpha$

$x^2 = 244 - 240\cos \alpha$

$x^2 = 244 - 240\cos (\theta + 90^\circ)$

$x^2 = 244 - 240(\cos \theta \cos 90^\circ - \sin \theta \sin 90^\circ)$

$x^2 = 244 + 240\sin \theta$   →   Equation (1)
 

From right triangle ABD:
$x^2 + 8^2 = (2r)^2$

$x^2 = 4r^2 - 64$

$\sin \theta = \dfrac{8}{2r}$

$\sin \theta = \dfrac{4}{r}$
 

From Equation (1)
$4r^2 - 64 = 244 + 240\left( \dfrac{4}{r} \right)$

$4r^2 - 308 - \dfrac{960}{r} = 0$

$r^3 - 77r - 240 = 0$   →   Equation (2)

$r = 10.0446, \,\, -3.8691, \,\, -6.1755$
 

Use r = 10.0446 cm           answer

$b = 10$

$c = 12$   and

$d = 2r$
 

From right triangle ACD:
${d_1}^2 + 12^2 = (2r)^2$

$d_1 = \sqrt{4r^2 - 144}$
 

From right triangle ABD:
${d_2}^2 + 8^2 = (2r)^2$

$d_2 = \sqrt{4r^2 - 64}$
 

By Ptolemy's Theorem for cyclic quadrilaterals:
$d_1 \, d_2 = ac + bd$

$\left( \sqrt{4r^2 - 144} \right)\left(\sqrt{4r^2 - 64} \right) = 8(12) + 10(2r)$

$\sqrt{(4r^2 - 144)(4r^2 - 64)} = 96 + 20r$

$(4r^2 - 144)(4r^2 - 64) = (96 + 20r)^2$

$(r^2 - 36)(r^2 - 16) = (24 + 5r)^2$

$r^4 - 52r^2 + 576 = 576 + 240r + 25r^2$

$r^4 - 77r^2 - 240r = 0$

$r^3 - 77r - 240 = 0$   →   See Equation (2) in the first solution   (Okay! )