Relationship Between Central Angle and Inscribed Angle
Central angle = Angle subtended by an arc of the circle from the center of the circle.
Inscribed angle = Angle subtended by an arc of the circle from any point on the circumference of the circle. Also called circumferential angle and peripheral angle.
Figure below shows a central angle and inscribed angle intercepting the same arc AB. The relationship between the two is given by
if and only if both angles intercepted the same arc. In the figure below, θ and α intercepted the same arc AB.
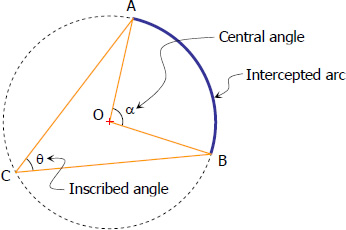
Click here for the proof of the relationship.
Some Applications of the Relationship
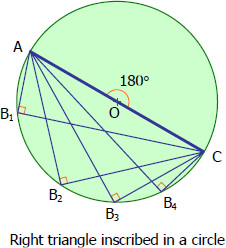
• Right Triangle Inscribed in a Circle
We can also say that an angle inscribed in a semicircle is a right angle. From the figure above, the diameter AC is the hypotenuse of triangles AB1C, AB2C, AB3C, and AB4C.
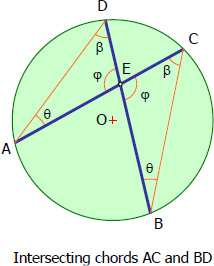
$\dfrac{\text{opposite to } \theta}{\text{opposite to } \beta} = \dfrac{DE}{AE} = \dfrac{CE}{BE}$
$BE \times DE = AE \times CE$
This means that for intersecting chords in a circle, the product of segments of one is equal to the product of segments of the other.
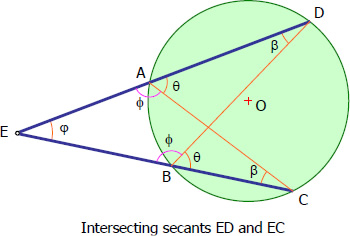
Therefore, triangles EAC and EBD are similar, and by ratio and proportion of similar triangles
$\dfrac{\text{opposite to } \varphi}{\text{opposite to } \beta} = \dfrac{DE}{BE} = \dfrac{CE}{AE}$
$DE \times AE = CE \times BE$
Also note that
$\varphi = \frac{1}{2}(\theta - \beta)$
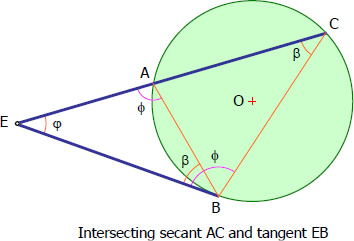
• Intersecting Tangent and Secant
Triangle ABE is similar to triangle BCE. By ratio and proportion
$\dfrac{\text{opposite to } \varphi}{\text{opposite to } \beta} = \dfrac{BE}{AE} = \dfrac{CE}{BE}$
$BE^2 = CE \times AE$
- Log in to post comments