If you have questions about the angle θ shown in the figure, see the
relationship between inscribed angle and central angle.
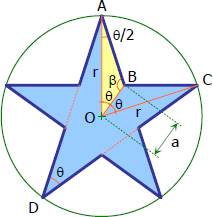From the figure shown:
$2\theta = \frac{1}{5}(360^\circ) = 72^\circ$
$\theta = 36^\circ$
$\frac{1}{2}\theta = 18^\circ$
From triangle ABO:
$\theta + \frac{1}{2}\theta + \beta = 180^\circ$
$36^\circ + 18^\circ + \beta = 180^\circ$
$\beta = 126^\circ$
By Sine Law
$\dfrac{a}{\sin \frac{1}{2}\theta} = \dfrac{r}{\sin \beta}$
$\dfrac{a}{\sin 18^\circ} = \dfrac{20}{\sin 126^\circ}$
$a = 7.64 \, \text{ cm }$
Area of triangle ABO:
$A_{ABO} = \frac{1}{2}ar \, \sin \theta$
$A_{ABO} = \frac{1}{2}(7.64)(20) \, \sin 36^\circ$
$A_{ABO} = 44.903 \, \text{ cm}^2$
Area of Pentagram (the five-pointed star)
$A = 10\,A_{ABO}$
$A = 10(44.903)$
$A = 449.03 \, \text{ cm}^2$ answer
