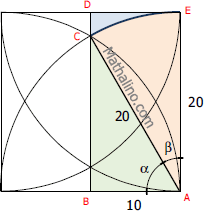
From triangle ABC
$\cos \alpha = \dfrac{10}{20}$
$\alpha = 60^\circ$
At corner A
$\beta = 90^\circ - \alpha = 90^\circ - 60^\circ$
$\beta = 30^\circ$
Area of rectangle ABDE
$A_{ABDE} = 20(10)$
$A_{ABDE} = 200 \, \text{ cm}^2$
Area of triangle ABC
$A_{ABC} = \frac{1}{2}(10)(20) \sin \alpha = 100 \sin 60^\circ$
$A_{ABC} = 50\sqrt{3} \, \text{ cm}^2$
Area of sector ACE
$A_{ACE} = \dfrac{\pi r^2 \beta_{deg}}{360^\circ} = \dfrac{\pi (20^2)(30^\circ)}{360^\circ}$
$A_{ACE} = \frac{100}{3}\pi \, \text{ cm}^2$
Area of CED
$A_{CED} = A_{ABDE} - A_{ABC} - A_{ACE}$
$A_{CED} = 200 - 50\sqrt{3} - \frac{100}{3}\pi$
$A_{CED} = 8.68 \, \text{ cm}^2$
A similar problem that involves the same area as ACED was solved using integration. Look for the solution of area ABC in the following link: Solution by integration.
Required Area
$A_{required} = A_{square} - 8A_{CED}$
$A_{required} = 20^2 - 8(8.68)$
$A_{required} = 330.56 \, \text{ cm}^2$ answer
