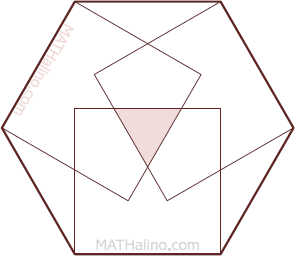
10 Area common to three squares inside the regular hexagon
Problem
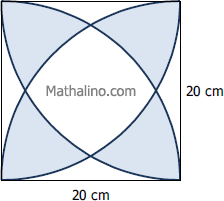
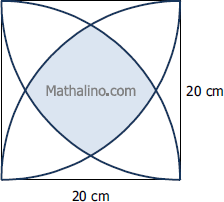
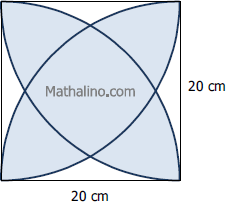
Three squares are drawn so that each will contain a side of regular hexagon as shown in the given figure. If the hexagon has a perimeter of 60 in., compute the area of the region common to the three squares. The required area is the shaded region in the figure.