Area bounded by arcs of quarter circles

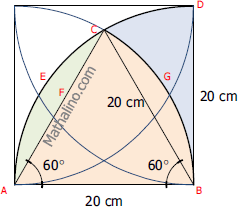
Area of quarter circle AECDB
$A_{AECDB} = \frac{1}{4}\pi (20^2) = 100\pi \, \text{ cm}^2$

$A_{AECDB} = 314.16 \, \text{ cm}^2$
 

Area of sector AFCGB
$A_{AFCGB} = \frac{1}{6}\pi (20^2) = \frac{200}{3}\pi \, \text{ cm}^2$

$A_{AFCGB} = 209.44 \, \text{ cm}^2$
 

Area of segment AFCE
$A_{AFCE} = \frac{1}{6}\pi (20^2) - \frac{1}{2}(20^2)\sin 60^\circ$

$A_{AFCE} = \frac{200}{3}\pi - 100\sqrt{3} \, \text{ cm}^2$

$A_{AFCE} = 36.23 \, \text{ cm}^2$
 

Area of BGCD
$A_{BGCD} = A_{AECDB} - A_{AFCGB} - A_{AFCE}$

$A_{BGCD} = 314.16 - 209.44 - 36.23$

$A_{BGCD} = 68.49 \, \text{ cm}^2$
 

Required Area
 

 

$A_{required} = A_{square} - 4A_{BGCD} = 20^2 - 4(68.49)$

$A_{required} = 126.04 \, \text{ cm}^2$           answer

From triangle BED
$\cos (30^\circ + 15^\circ) = \dfrac{10}{x}$

$x = \dfrac{10}{\cos 45^\circ} = 10\sqrt{2} \, \text{ cm}$
 

Area of sector DAC
$A_{DAC} = \dfrac{\pi(20^2)(15^\circ + 15^\circ)}{360^\circ} = \dfrac{100\pi}{3} \text{ cm}^2$

$A_{DAC} = 104.72 \, \text{ cm}^2$
 

Area of triangle DBC
$A_{DBC} = \frac{1}{2}(20x) \sin 15^\circ = \frac{1}{2}(20)(10\sqrt{2}) \sin 15^\circ$

$A_{DBC} = 36.60 \, \text{ cm}^2$
 

Area of ABC
$A_{ABC} = A_{DAC} - 2A_{DBC} = 104.72 - 2(36.60)$

$A_{ABC} = 31.52 \, \text{ cm}^2$
 

Required Area
 

 

$A_{required} = 4A_{ABC} = 4(31.52)$

$A_{required} = 126.08 \, \text{ cm}^2$           answer

This problem was solved using integration. See it here: /node/2989