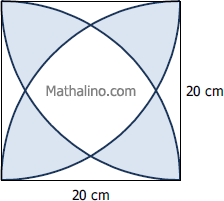
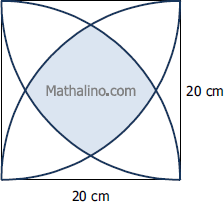
Area inside a circle but outside three other externally tangent circles
Problem 11
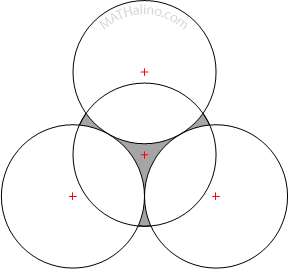
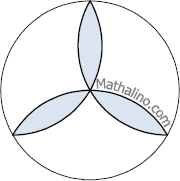
Three identical circles of radius 30 cm are tangent to each other externally. A fourth circle of the same radius was drawn so that its center is coincidence with the center of the space bounded by the three tangent circles. Find the area of the region inside the fourth circle but outside the first three circles. It is the shaded region shown in the figure below.