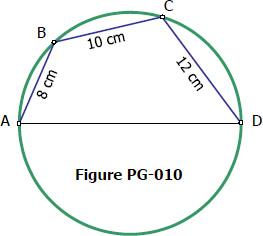
Derivation / Proof of Ptolemy's Theorem for Cyclic Quadrilateral
Ptolemy's theorem for cyclic quadrilateral states that the product of the diagonals is equal to the sum of the products of opposite sides. From the figure below, Ptolemy's theorem can be written as
$d_1 d_2 = ac + bd$
Quadrilateral with one side as diameter of circumscribing circle
Problem PG-010
The quadrilateral ABCD shown in Fig. PG-010 is inscribed in a circle with side AD coinciding with the diameter of the circle. if sides AB, BC, and CD are 8 cm, 10 cm, and 12 cm long, respectively, find the radius of the circumscribing circle.
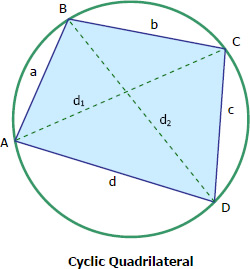
The Cyclic Quadrilateral
A quadrilateral is said to be cyclic if its vertices all lie on a circle. In cyclic quadrilateral, the sum of two opposite angles is 180° (or π radian); in other words, the two opposite angles are supplementary.
$A + C = 180^\circ$
$B + D = 180^\circ$
- Read more about The Cyclic Quadrilateral
- Log in or register to post comments