Quadrilateral with one side as diameter of circumscribing circle

based on the relationship between central and inscribed angles, the figure below show the relationship between angle ADB (θ) and angle AOB (2θ) and the obtuse angle BCD (α) and reflex angle BOD (2α).
 

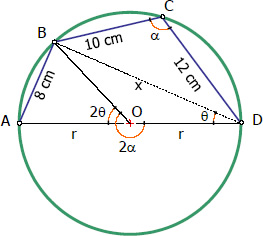From the figure:
$2\alpha = 2\theta + 180^\circ$

$\alpha = \theta + 90^\circ$
 

From triangle BCD (Using Cosine Law):

$x^2 = 10^2 + 12^2 - 2(10)(12)\cos \alpha$

$x^2 = 244 - 240\cos \alpha$

$x^2 = 244 - 240\cos (\theta + 90^\circ)$

$x^2 = 244 - 240(\cos \theta \cos 90^\circ - \sin \theta \sin 90^\circ)$

$x^2 = 244 + 240\sin \theta$   →   Equation (1)
 

From right triangle ABD:
$x^2 + 8^2 = (2r)^2$

$x^2 = 4r^2 - 64$

$\sin \theta = \dfrac{8}{2r}$

$\sin \theta = \dfrac{4}{r}$
 

From Equation (1)
$4r^2 - 64 = 244 + 240\left( \dfrac{4}{r} \right)$

$4r^2 - 308 - \dfrac{960}{r} = 0$

$r^3 - 77r - 240 = 0$   →   Equation (2)

$r = 10.0446, \,\, -3.8691, \,\, -6.1755$
 

Use r = 10.0446 cm           answer

$a = 8$

$b = 10$

$c = 12$   and

$d = 2r$
 

From right triangle ACD:
${d_1}^2 + 12^2 = (2r)^2$

$d_1 = \sqrt{4r^2 - 144}$
 

From right triangle ABD:
${d_2}^2 + 8^2 = (2r)^2$

$d_2 = \sqrt{4r^2 - 64}$
 

By Ptolemy's Theorem for cyclic quadrilaterals:
$d_1 \, d_2 = ac + bd$

$\left( \sqrt{4r^2 - 144} \right)\left(\sqrt{4r^2 - 64} \right) = 8(12) + 10(2r)$

$\sqrt{(4r^2 - 144)(4r^2 - 64)} = 96 + 20r$

$(4r^2 - 144)(4r^2 - 64) = (96 + 20r)^2$

$(r^2 - 36)(r^2 - 16) = (24 + 5r)^2$

$r^4 - 52r^2 + 576 = 576 + 240r + 25r^2$

$r^4 - 77r^2 - 240r = 0$

$r^3 - 77r - 240 = 0$   →   See Equation (2) in the first solution   (Okay! )