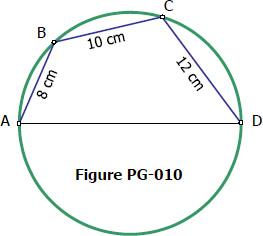
Derivation / Proof of Ptolemy's Theorem for Cyclic Quadrilateral
Ptolemy's theorem for cyclic quadrilateral states that the product of the diagonals is equal to the sum of the products of opposite sides. From the figure below, Ptolemy's theorem can be written as
Derivation of Formula for Area of Cyclic Quadrilateral
For a cyclic quadrilateral with given sides a, b, c, and d, the formula for the area is given by
Where s = (a + b + c + d)/2 known as the semi-perimeter.
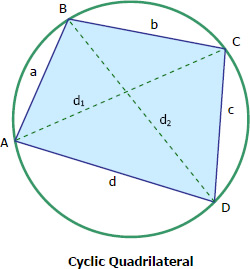
The Cyclic Quadrilateral
A quadrilateral is said to be cyclic if its vertices all lie on a circle. In cyclic quadrilateral, the sum of two opposite angles is 180° (or π radian); in other words, the two opposite angles are supplementary.
$B + D = 180^\circ$
- Read more about The Cyclic Quadrilateral
- Log in to post comments
The Quadrilateral
Quadrilateral is a polygon of four sides and four vertices. It is also called tetragon and quadrangle. In the triangle, the sum of the interior angles is 180°; for quadrilaterals the sum of the interior angles is always equal to 360°
Classifications of Quadrilaterals
There are two broad classifications of quadrilaterals; simple and complex. The sides of simple quadrilaterals do not cross each other while two sides of complex quadrilaterals cross each other.
Simple quadrilaterals are further classified into two: convex and concave. Convex if none of the sides pass through the quadrilateral when prolonged while concave if the prolongation of any one side will pass inside the quadrilateral.
- Read more about The Quadrilateral
- Log in to post comments