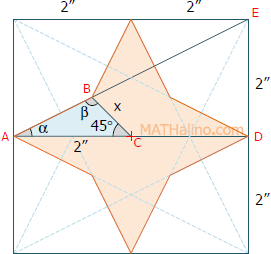
From the right triangle ADE
$\tan \alpha = 2/4$
$\alpha = 26.565^\circ$
From triangle ABC
$\beta = 180^\circ - 45^\circ - \alpha$
$\beta = 180^\circ - 45^\circ - 26.565^\circ$
$\beta = 108.435^\circ$
By Sine law
$\dfrac{x}{\sin \alpha} = \dfrac{2}{\sin \beta}$
$\dfrac{x}{\sin 26.565^\circ} = \dfrac{2}{\sin 108.435^\circ}$
$x = 0.9428 \, \text{ in.}$
Area of triangle ABC
$A_{ABC} = \frac{1}{2}(2x) \sin 45^\circ$
$A_{ABC} = \frac{1}{2}(2)(0.9428) \sin 45^\circ$
$A_{ABC} = 0.6667 \, \text{ in.}^2$
Required area
$A = 8A_{ABC} = 8(0.6667)$
$A = 5.33 \, \text{ in.}^2$ answer
