Derivation of Cosine Law
The following are the formulas for cosine law for any triangles with sides a, b, c and angles A, B, C, respectively.
$a^2 = b^2 + c^2 - 2bc\cos A$
$b^2 = a^2 + c^2 - 2ac\cos B$
$c^2 = a^2 + b^2 - 2ab\cos C$
Derivation:
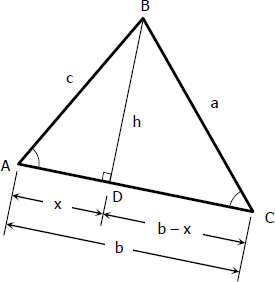Consider the triangle to the right:
Cosine function for triangle ADB
$\cos A = \dfrac{x}{c}$
$x = c\cos A$
Pythagorean theorem for triangle ADB
$x^2 + h^2 = c^2$
$h^2 = c^2 - x^2$
Pythagorean theorem for triangle CDB
$(b - x)^2 + h^2 = a^2$
Substitute h2 = c2 - x2
$(b - x)^2 + (c^2 - x^2) = a^2$
$(b^2 - 2bx + x^2) + (c^2 - x^2) = a^2$
$b^2 - 2bx + c^2 = a^2$
Substitute x = c cos A
$b^2 - 2b(c \cos A) + c^2 = a^2$
Rearrange:
$a^2 = b^2 + c^2 - 2bc\cos A$
The other two formulas can be derived in the same manner.