Derivation of Sum and Difference of Two Angles

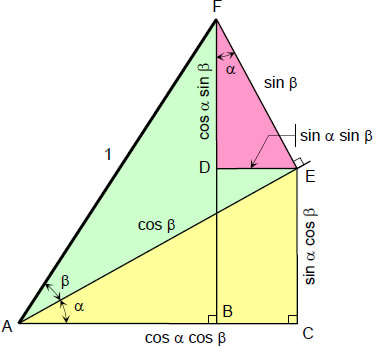
The sum and difference of two angles can be derived from the figure shown below.
 

Consider triangle AEF:
$\cos \beta = \dfrac{\overline{AE}}{1}; \,\, \overline{AE} = \cos \beta$

$\sin \beta = \dfrac{\overline{EF}}{1}; \,\, \overline{EF} = \sin \beta$
 

From triangle EDF:
$\sin \alpha = \dfrac{\overline{DE}}{\overline{EF}}$

$\sin \alpha = \dfrac{\overline{DE}}{\sin \beta}$

$\overline{DE} = \sin \alpha \, \sin \beta$
 

$\cos \alpha = \dfrac{\overline{DF}}{\overline{EF}}$

$\cos \alpha = \dfrac{\overline{DF}}{\sin \beta}$

$\overline{DF} = \cos \alpha \, \sin \beta$
 

$\overline{BC} = \overline{DE} = \sin \alpha \, \sin \beta$
 

From Triangle ACE:
$\sin \alpha = \dfrac{\overline{CE}}{\overline{AE}}$

$\sin \alpha = \dfrac{\overline{CE}}{\cos \beta}$

$\overline{CE} = \sin \alpha \, \cos \beta$
 

$\cos \alpha = \dfrac{\overline{AC}}{\overline{AE}}$

$\cos \alpha = \dfrac{\overline{AC}}{\cos \beta}$

$\overline{AC} = \cos \alpha \, \cos \beta$
 

$\overline{BD} = \overline{CE} = \sin \alpha \, \cos \beta$
 

The summary of the above solution is shown below:
 

Sum of two angles
From triangle ABF:
$\sin (\alpha + \beta) = \overline{BD} + \overline{DF}$

$\cos (\alpha + \beta) = \overline{AC} - \overline{BC}$

$\tan (\alpha + \beta) = \dfrac{\sin (\alpha + \beta)}{\cos (\alpha + \beta)}$

$\tan (\alpha + \beta) = \dfrac{\sin \alpha \, \cos \beta + \cos \alpha \, \sin \beta}{\cos \alpha \, \cos \beta - \sin \alpha \, \sin \beta}$

$\tan (\alpha + \beta) = \dfrac{\dfrac{\sin \alpha \, \cos \beta}{\cos \alpha \, \cos \beta} + \dfrac{\cos \alpha \, \sin \beta}{\cos \alpha \, \cos \beta}}{\dfrac{\cos \alpha \, \cos \beta}{\cos \alpha \, \cos \beta} - \dfrac{\sin \alpha \, \sin \beta}{\cos \alpha \, \cos \beta}}$

$\tan (\alpha + \beta) = \dfrac{\dfrac{\sin \alpha}{\cos \alpha} + \dfrac{\sin \beta}{\cos \beta}}{1 - \dfrac{\sin \alpha}{\cos \alpha} \, \dfrac{\sin \beta}{\cos \beta}}$

Difference of two angles
Let β = -β and note that
sin (-β) = -sin β
cos (-β) = cos β and
tan (-β) = -tan β
 

$\sin [ \, \alpha + (-\beta) \, ] = \sin \alpha \, \cos (-\beta) + \cos \alpha \, \sin (-\beta)$

$\cos [ \, \alpha + (-\beta) \, ] = \cos \alpha \, \cos (-\beta) - \sin \alpha \, \sin (-\beta)$

$\tan [ \, \alpha + (-\beta) \, ] = \dfrac{\tan \alpha + \tan (-\beta)}{1 - \tan \alpha \, \tan (-\beta)}$