identities

Basic Identities
See the derivation of basic identities.

1. $\sin \theta = \dfrac{1}{\csc \theta} ~ \Leftrightarrow ~ \csc \theta = \dfrac{1}{\sin \theta}$
    
2. $\cos \theta = \dfrac{1}{\sec \theta} ~ \Leftrightarrow ~ \sec \theta = \dfrac{1}{\cos \theta}$
    
3. $\tan \theta = \dfrac{\sin \theta}{\cos \theta} = \dfrac{1}{\cot \theta} ~ \Leftrightarrow ~ \cot \theta = \dfrac{\cos \theta}{\sin \theta} = \dfrac{1}{\tan \theta}$

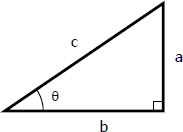In reference to the right triangle shown and from the functions of a right triangle:
a/c = sin θ
b/c = cos θ
c/b = sec θ
c/a = csc θ
a/b = tan θ
b/a = cot θ
 

The sum and difference of two angles can be derived from the figure shown below.
 

The Double Angle Formulas can be derived from Sum of Two Angles listed below:
$\sin (A + B) = \sin A \, \cos B + \cos A \, \sin B$   →   Equation (1)

$\cos (A + B) = \cos A \, \cos B - \sin A \, \sin B$   →   Equation (2)

$\tan (A + B) = \dfrac{\tan A + \tan B}{1 - \tan A \, \tan B}$   →   Equation (3)