Derivation of Basic Identities
The derivation of basic identities can be done easily by using the functions of a right triangle. For easy reference, these trigonometric functions are listed below.
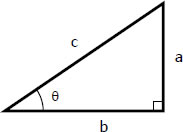 a/c = sin θ
a/c = sin θb/c = cos θ
a/b = tan θ
c/a = csc θ
c/b = sec θ
b/a = cot θ
Sine and Cosecant are reciprocal to each other
$\sin \theta = \dfrac{a}{c}$
$\sin \theta = \dfrac{a/a}{c/a}$
$\sin \theta = \dfrac{1}{\csc \theta}$
and
$\csc \theta = \dfrac{1}{\sin \theta}$
Cosine and Secant are reciprocal to each other
$\cos \theta = \dfrac{b}{c}$
$\cos \theta = \dfrac{b/b}{c/b}$
$\cos \theta = \dfrac{1}{\sec \theta}$
and
$\sec \theta = \dfrac{1}{\cos \theta}$
Tangent and Cotangent are reciprocal to each other and Tangent is the ratio of Sine to Cosine
$\tan \theta = \dfrac{a}{b}$
$\tan \theta = \dfrac{a/a}{b/a}$
$\tan \theta = \dfrac{1}{\cot \theta}$
$\tan \theta = \dfrac{a}{b}$
$\tan \theta = \dfrac{a/c}{b/c}$
$\tan \theta = \dfrac{\sin \theta}{\cos \theta}$
Thus,
$\tan \theta = \dfrac{\sin \theta}{\cos \theta} = \dfrac{1}{\cot \theta}$
and
$\cot \theta = \dfrac{\cos \theta}{\sin \theta} = \dfrac{1}{\tan \theta}$
