Derivation of Sine Law

For any triangles with vertex angles and corresponding opposite sides are A, B, C and a, b, c, respectively, the sine law is given by the formula...
 

Derivation
To derive the formula, erect an altitude through B and label it h_B as shown below. Expressing h_B in terms of the side and the sine of the angle will lead to the formula of the sine law.
 

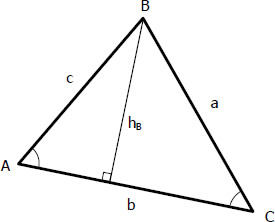
$\sin A = \dfrac{h_B}{c}$

$h_B = c \sin A$
 

$\sin C = \dfrac{h_B}{a}$

$h_B = a \sin C$
 

Equate the two h_B's above:
$h_B = h_B$

$c \sin A = a \sin C$

$\dfrac{c}{\sin C} = \dfrac{a}{\sin A}$
 

To include angle B and side b in the above relationship, construct an altitude through C and label it h_C as shown below.
 

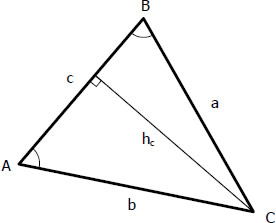
$\sin A = \dfrac{h_C}{b}$

$h_C = b \sin A$
 

$\sin B = \dfrac{h_C}{a}$

$h_C = a \sin B$
 

$h_C = h_C$

$b \sin A = a \sin B$

$\dfrac{b}{\sin B} = \dfrac{a}{\sin A}$
 

Thus,

Therefore, the ratio of one side to the sine of its opposite angle is constant.
 

Note:
The constant ratio above is the diameter of the circumscribing circle about the triangle. See the proof (not available for now) for this note.