If arcsin (3x - 4y) = 1.571 and arccos (x - y) = 1.047, what is the value of x?
Problem
If $\arcsin (3x - 4y) = 1.571$ and $\arccos (x - y) = 1.047$, what is the value of $x$?
| A. 0.5 | C. 1.5 |
| B. 1.0 | D. 2.0 |
 MATHalinoEngineering Math Review
MATHalinoEngineering Math ReviewProblem
If $\arcsin (3x - 4y) = 1.571$ and $\arccos (x - y) = 1.047$, what is the value of $x$?
| A. 0.5 | C. 1.5 |
| B. 1.0 | D. 2.0 |
Problem
The tide in Bay of Fundy rises and falls every 13 hours. The depth of the water at a certain point in the bay is modeled by a function d = 5 sin (2π/13)t + 9, where t is time in hours and d is depth in meters. Find the depth at t = 13/4 (high tide) and t = 39/4 (low tide).
Problem
The number of hours daylight, D(t) at a particular time of the year can be approximated by
for t days and t = 0 corresponding to January 1. The constant K determines the total variation in day length and depends on the latitude of the locale. When is the day length the longest, assuming that it is NOT a leap year?
| A. December 20 | C. June 20 |
| B. June 19 | D. December 19 |
The following are the formulas for cosine law for any triangles with sides a, b, c and angles A, B, C, respectively.
$b^2 = a^2 + c^2 - 2ac\cos B$
$c^2 = a^2 + b^2 - 2ab\cos C$
For any triangles with vertex angles and corresponding opposite sides are A, B, C and a, b, c, respectively, the sine law is given by the formula...
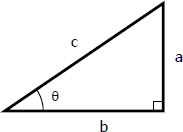 In reference to the right triangle shown and from the functions of a right triangle:
In reference to the right triangle shown and from the functions of a right triangle:
a/c = sin θ
b/c = cos θ
c/b = sec θ
c/a = csc θ
a/b = tan θ
b/a = cot θ
 The sum and difference of two angles can be derived from the figure shown below.
The sum and difference of two angles can be derived from the figure shown below.
The Double Angle Formulas can be derived from Sum of Two Angles listed below:
$\sin (A + B) = \sin A \, \cos B + \cos A \, \sin B$ → Equation (1)
$\cos (A + B) = \cos A \, \cos B - \sin A \, \sin B$ → Equation (2)
$\tan (A + B) = \dfrac{\tan A + \tan B}{1 - \tan A \, \tan B}$ → Equation (3)
Pythagorean Theorem
In any right triangle, the sum of the square of the two perpendicular sides is equal to the square of the longest side. For a right triangle with legs measures $a$ and $b$ and length of hypotenuse $c$, the theorem can be expressed in the form