Derivation of Pythagorean Identities

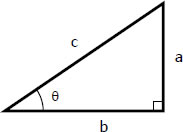In reference to the right triangle shown and from the functions of a right triangle:
a/c = sin θ
b/c = cos θ
c/b = sec θ
c/a = csc θ
a/b = tan θ
b/a = cot θ
 

From Pythagorean Theorem
$a^2 + b^2 = c^2$

$\dfrac{a^2}{c^2} + \dfrac{b^2}{c^2} = \dfrac{c^2}{c^2}$

$\left( \dfrac{a}{c} \right)^2 + \left( \dfrac{b}{c} \right)^2 = 1$

$(\sin \theta)^2 + (\cos \theta)^2 = 1$

$a^2 + b^2 = c^2$

$\dfrac{a^2}{b^2} + \dfrac{b^2}{b^2} = \dfrac{c^2}{b^2}$

$\left( \dfrac{a}{b} \right)^2 + 1 = \left( \dfrac{c}{b} \right)^2$

$(\tan \theta)^2 + 1 = (\sec \theta)^2$

$a^2 + b^2 = c^2$

$\dfrac{a^2}{a^2} + \dfrac{b^2}{a^2} = \dfrac{c^2}{a^2}$

$1 + \left( \dfrac{b}{a} \right)^2 \left( \dfrac{c}{a} \right)^2$

$1 + (\cot \theta)^2 = (\csc \theta)^2$

Another way to derive tan² θ + 1 = sec² θ
$\sin^2 \theta + \cos^2 \theta = 1$

$\dfrac{\sin^2 \theta}{\cos^2 \theta} + \dfrac{\cos^2 \theta}{\cos^2 \theta} = \dfrac{1}{\cos^2 \theta}$

$\left( \dfrac{\sin \theta}{\cos \theta} \right)^2 + 1 = \left( \dfrac{1}{\cos \theta} \right)^2$

$(\tan \theta)^2 + 1 = (\sec \theta)^2$

$\tan^2 \theta + 1 = \sec^2 \theta$       (okay!)
 

Another way to derive 1 + cot² θ = csc² θ
$\sin^2 \theta + \cos^2 \theta = 1$

$\dfrac{\sin^2 \theta}{\sin^2 \theta} + \dfrac{\cos^2 \theta}{\sin^2 \theta} = \dfrac{1}{\sin^2 \theta}$

$1 + \left( \dfrac{\cos \theta}{\sin \theta} \right)^2 = \left( \dfrac{1}{\sin \theta} \right)^2$

$1 + (\cot \theta)^2 = (\csc \theta)^2$

$1 + \cot^2 \theta = \csc^2 \theta$       (okay!)