Problem
A circle has an equation of $x^2 + y^2 + 2cy = 0$. Find the value of $c$ when the length of the tangent from (5, 4) to the circle is equal to one.
| A. 5 | C. 3 |
| B. -3 | D. -5 |
Problem 10
In a triangle ABC, if $\dfrac{2 \cos A}{a} + \dfrac{\cos B}{b} + \dfrac{2 \cos C}{c} = \dfrac{a}{bc} + \dfrac{b}{ca}$, find the value of angle $A$.
Problem 26
A kite is 40 ft high with 50 ft cord out. If the kite moves horizontally at 5 miles per hour directly away from the boy flying it, how fast is the cord being paid out?
Problem 11
A train starting at noon, travels north at 40 miles per hour. Another train starting from the same point at 2 PM travels east at 50 miles per hour. Find, to the nearest mile per hour, how fast the two trains are separating at 3 PM.
Problem 10
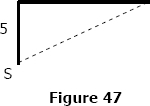A boy on a bike rides north 5 mi, then turns east (Fig. 47). If he rides 10 mi/hr, at what rate does his distance to the starting point S changing 2 hour after he left that point?
Problem 06
A ladder 20 ft long leans against a vertical wall. If the top slides downward at the rate of 2 ft/sec, find how fast the lower end is moving when it is 16 ft from the wall.
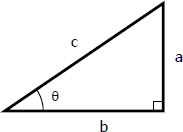In reference to the right triangle shown and from the functions of a right triangle:
a/c = sin θ
b/c = cos θ
c/b = sec θ
c/a = csc θ
a/b = tan θ
b/a = cot θ
Pythagorean Theorem
In any right triangle, the sum of the square of the two perpendicular sides is equal to the square of the longest side. For a right triangle with legs measures $a$ and $b$ and length of hypotenuse $c$, the theorem can be expressed in the form
