Derivation of Pythagorean Theorem

Tags: 
derivation of formula
trigonometry
Pythagora
Pythagorean theorem
bhaskara
james garfield

Pythagorean Theorem
In any right triangle, the sum of the square of the two perpendicular sides is equal to the square of the longest side. For a right triangle with legs measures $ a $ and $ b $ and length of hypotenuse $ c $, the theorem can be expressed in the form
 

$ a^2 + b^2 = c^2 $

 

Proved by Pythagoras
 

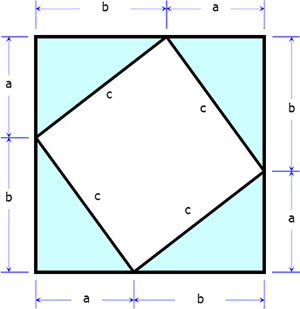
Proof of Pythagorean Theorem by Pythagoras

 

Area of the large square = Area of four triangles + Area of small square
$ A_{total} = A_{four \, \, triangles} + A_{small \, \, square} $

$ (a + b)^2 = 4 \, \left( \frac{1}{2} ab \right) + c^2 $

$ a^2 + 2ab + b^2 = 2ab + c^2 $

$ a^2 + b^2 = c^2 $
 

Proved by Bhaskara
Bhaskara (1114 - 1185) was an Indian mathematician and astronomer.
 

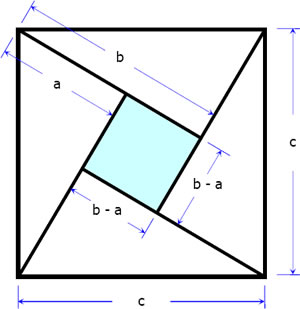
Proof by Bhaskara

 

Area of the large square = Area of four triangles + Area of inner (smaller) square
$ A_{total} = A_{four \, \, triangles} + A_{small \, \, square} $

$ c^2 = 4 \, \left( \frac{1}{2} ab \right) + (b - a)^2 $

$ c^2 = 2ab + (b^2 - 2ab + a^2) $

$ c^2 = 2ab + b^2 - 2ab + a^2 $

$ c^2 = b^2 + a^2 $
 

Proved by U.S. Pres. James Garfield
 

Proof by Pres. James Garfield

 

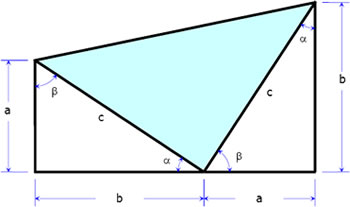
Area of trapezoid = Area of 3 triangles
$ \frac{1}{2}(a + b)(a + b) = \frac{1}{2}ab + \frac{1}{2}c^2 + \frac{1}{2}ab $

$ (a + b)^2 = ab + c^2 + ab $

$ a^2 + 2ab + b^2 = 2ab + c^2 $

$ a^2 + b^2 = c^2 $
 

»
SPONSORED LINKS


Page copy protected against web site content infringement by Copyscape

Recent comments