Trigonometric Identities

Half angle formulas can be derived from the double angle formulas, particularly, the cosine of double angle. For easy reference, the cosines of double angle are listed below:
 

Note that the equations above are identities, meaning, the equations are true for any value of the variable θ. The key on the derivation is to substitute θ with ½ θ.
 

The derivation of basic identities can be done easily by using the functions of a right triangle. For easy reference, these trigonometric functions are listed below.

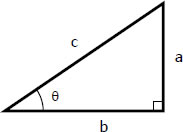a/c = sin θ
b/c = cos θ
a/b = tan θ
c/a = csc θ
c/b = sec θ
b/a = cot θ

Basic Identities
See the derivation of basic identities.

1. $\sin \theta = \dfrac{1}{\csc \theta} ~ \Leftrightarrow ~ \csc \theta = \dfrac{1}{\sin \theta}$
    
2. $\cos \theta = \dfrac{1}{\sec \theta} ~ \Leftrightarrow ~ \sec \theta = \dfrac{1}{\cos \theta}$
    
3. $\tan \theta = \dfrac{\sin \theta}{\cos \theta} = \dfrac{1}{\cot \theta} ~ \Leftrightarrow ~ \cot \theta = \dfrac{\cos \theta}{\sin \theta} = \dfrac{1}{\tan \theta}$

The sum and difference of two angles can be derived from the figure shown below.