Functions of a Right Triangle

Tags: 
right triangle

From the right triangle shown below,
 

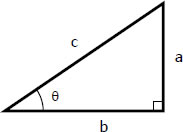
Right triangle with sides a, b, and c and angle theta

 

the trigonometric functions of angle θ are defined as follows:

$ \sin \theta = \dfrac{opposite\,\,side}{hypotenuse} = \dfrac{a}{c} $
$ \cos \theta = \dfrac{adjacent\,\,side}{hypotenuse} = \dfrac{b}{c} $
$ \tan \theta = \dfrac{opposite\,\,side}{adjacent\,\,side} = \dfrac{a}{b} $
$ \csc \theta = \dfrac{hypotenuse}{opposite\,\,side} = \dfrac{c}{a} $
$ \sec \theta = \dfrac{hypotenuse}{adjacent\,\,side} = \dfrac{c}{b} $
$ \cot \theta = \dfrac{adjacent\,\,side}{opposite\,\,side} = \dfrac{b}{a} $
 

The above relationships can be written into acronym soh-cah-toa-cho-sha-cao.

  1. soh = sine of theta is equal to opposite side over the hypotenuse.
  2. cah = cosine of theta is equal to adjacent side over the hypotenuse.
  3. toa = tangent of theta is equal to opposite side over the adjacent side.
  4. cho = cosecant of theta is equal to hypotenuse over the opposite side.
  5. sha = secant of theta is equal to hypotenuse over the adjacent side.
  6. cao = cotangent of theta is equal to adjacent side over the opposite side.

See how these relationships were used to derive the Pythagorean identities.
 

»
SPONSORED LINKS


Page copy protected against web site content infringement by Copyscape

Recent comments