Example 01: Required Steel Area of Reinforced Concrete Beam
Problem
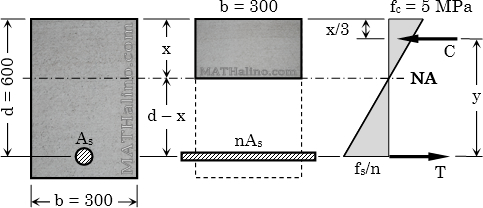
A rectangular concrete beam is reinforced in tension only. The width is 300 mm and the effective depth is 600 mm. The beam carries a moment of 80 kN·m which causes a stress of 5 MPa in the extreme compression fiber of concrete. Use n = 9.
1. What is the distance of the neutral axis from the top of the beam?
2. Calculate the required area for steel reinforcement.
3. Find the stress developed in the steel.

Recent comments