Design of Steel Reinforcement of Concrete Beams by WSD Method
Steps is for finding the required steel reinforcements of beam with known Mmax and other beam properties using Working Stress Design method.
Given the following, direct or indirect:
Effective depth = d
Allowable stress for concrete = fc
Allowable stress for steel = fs
Modular ratio = n
Maximum moment carried by the beam = Mmax
Step 1: Solve for the balanced moment capacity
$C_{bal} = \frac{1}{2}f_c \, bx_{bal}$
$M_{bal} = C_{bal}(d - \frac{1}{3}x_{bal})$
- If Mmax ≤ Mbal, design the beam as singly reinforced (go to Step 2)
- If Mmax > Mbal, design the beam as doubly reinforced (go to Step 3)
Step 2: Singly Reinforced Beam (Mmax ≤ Mbal)
$\dfrac{bx^3}{3} + \dfrac{bx^2(d - x)}{2} = \dfrac{nM_{max}(d - x)}{f_s}$
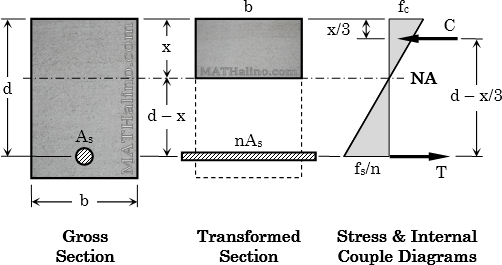
$A_s = \dfrac{bx^2}{2n(d - x)}$
You can also use the approximate formula for the amount of As
$A_s = \dfrac{M_{max}}{f_s(d - \frac{1}{3}x_{bal})}$
Step 3: Doubly Reinforced Beam (Mmax > Mbal)
Additional given: Embedment depth of compresion steel = d'
$A_{s1} = \dfrac{M_{bal}}{f_s(d - \frac{1}{3}x_{bal})}$
Solve As2 from the excess of Mmax and Mbal
$M_{excess} = M_{max} - M_{bal}$
$A_{s2} = \dfrac{M_{excess}}{f_s(d - d')}$
Total steel area in tension
$A_s = A_{s1} + A_{s2}$
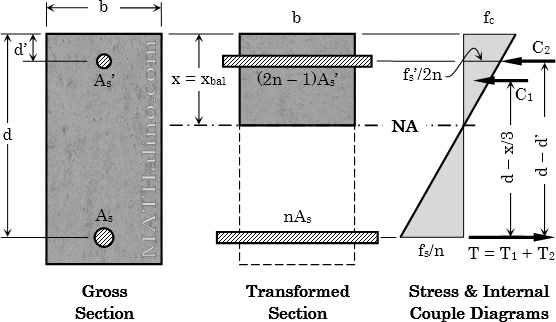
(Note: if fs' > fs, use fs' = fs)
$f_s' = \dfrac{2nf_c(x_{bal} - d')}{x_{bal}}$ or $f_s' = \dfrac{2f_s(x_{bal} - d')}{d - x_{bal}}$
$A_s' = \dfrac{2n \, M_{excess}}{f_s'(2n - 1)(d - d')}$
- Add new comment
- 66902 reads