Doubly Reinforced Beam

Problem
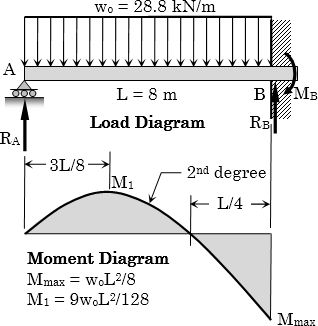
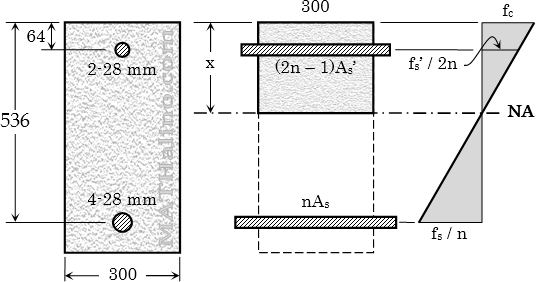
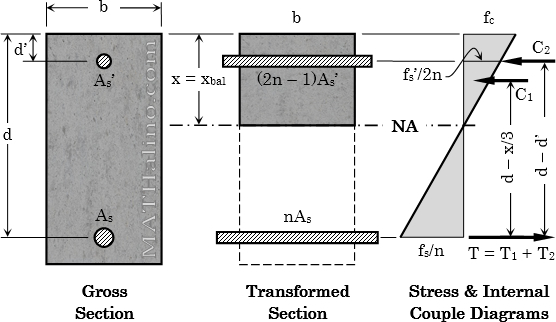
A propped beam 8 m long is to support a total load of 28.8 kN/m. It is desired to find the steel reinforcements at the most critical section in bending. The cross section of the concrete beam is 400 mm by 600 mm with an effective cover of 60 mm for the reinforcements. f’_c = 21 MPa, f_s = 140 MPa, n = 9. Determine the required number of 32 mm ø tension bars and the required number of 32 mm ø compression bars.
 

Problem
A 300 mm × 600 mm reinforced concrete beam section is reinforced with 4 - 28-mm-diameter tension steel at d = 536 mm and 2 - 28-mm-diameter compression steel at d' = 64 mm. The section is subjected to a bending moment of 150 kN·m. Use n = 9.

1. Find the maximum stress in concrete.
2. Determine the stress in the compression steel.
3. Calculate the stress in the tension steel.
 

Steps is for finding the required steel reinforcements of beam with known M_max and other beam properties using Working Stress Design method.

Given the following, direct or indirect: