Singly Reinforced Beam

Problem
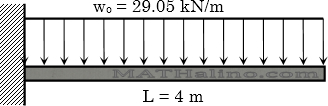
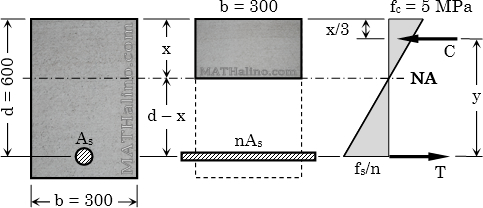
A reinforced concrete cantilever beam 4 m long has a cross-sectional dimensions of 400 mm by 750 mm. The steel reinforcement has an effective depth of 685 mm. The beam is to support a superimposed load of 29.05 kN/m including its own weight. Use f’_c = 21 MPa, f_s = 165 MPa, and n = 9. Determine the required number of 28 mm ø reinforcing bars using Working Stress Design method.
 

Problem
A reinforced concrete beam 300 mm wide has an effective depth of 600 mm. It is reinforced with 4-32 mm diameter bars for tension. f’_c = 21 MPa and f_y = 275 MPa. Find the moment capacity of the beam.
 

Problem
A rectangular reinforced concrete beam with width of 250 mm and effective depth of 500 mm is subjected to 150 kN·m bending moment. The beam is reinforced with 4 – 25 mm ø bars. Use alternate design method and modular ratio n = 9.

1. What is the maximum stress of concrete?
2. What is the maximum stress of steel?
3. What is the total compressive force in concrete?

Problem
A rectangular concrete beam is reinforced in tension only. The width is 300 mm and the effective depth is 600 mm. The beam carries a moment of 80 kN·m which causes a stress of 5 MPa in the extreme compression fiber of concrete. Use n = 9.
1.   What is the distance of the neutral axis from the top of the beam?
2.   Calculate the required area for steel reinforcement.
3.   Find the stress developed in the steel.
 

Steps is for finding the required steel reinforcements of beam with known M_max and other beam properties using Working Stress Design method.

Given the following, direct or indirect: