Working Stress Analysis for Concrete Beams

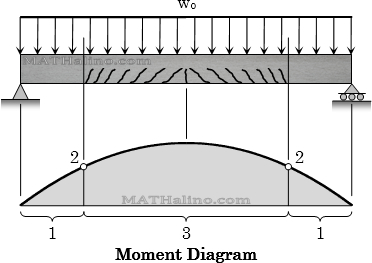
Consider a relatively long simply supported beam shown below. Assume the load w_o to be increasing progressively until the beam fails. The beam will go into the following three stages:

1. Uncrack Concrete Stage – at this stage, the gross section of the concrete will resist the bending which means that the beam will behave like a solid beam made entirely of concrete.
2. Crack Concrete Stage – Elastic Stress range
3. Ultimate Stress Stage – Beam Failure

 

Back to top

Concrete Beam Crack Stages

At section 1: Uncrack stage

1. Actual moment, M < Cracking moment, M_cr
2. No cracking occur
3. The gross section resists bending
4. The tensile stress of concrete is below rupture

 

At Section 2: Boundary between crack and uncrack stages

1. Actual moment, M = Cracking moment, M_cr
2. Crack begins to form
3. The gross section resists bending
4. The tensile stress of concrete reached the rupture point

 

At Section 3: Crack concrete stage

1. Actual moment, M > Cracking moment, M_cr
2. Elastic stress stage
3. Cracks developed at the tension fiber of the beam and spreads quickly to the neutral axis
4. The tensile stress of concrete is higher than the rupture strength
5. Ultimate stress stage can occur at failure

 

Back to top

Working Stress Analysis – Uncracked Stage

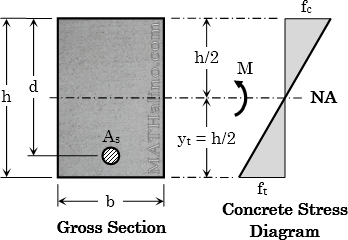
The beam will behave elastically and remains uncracked. The tensile stress of concrete is below rupture.
 

 

Cracking Moment
NSCP 2010, Section 409.6.2.3
 

Modulus of rupture of concrete, $f_r = 0.7\sqrt{f'_c} ~ \text{MPa}$

Cracking moment, $M_{cr} = \dfrac{f_r \, I_g}{y_t}$
 

Where
$I_g$ = Moment of inertia of the gross section neglecting reinforcement

$y_t$ = distance from centroid of gross section to extreme tension fiber
 

Back to top

Working Stress Analysis – Cracked Stage

General Requirement
Actual Stresses ≤ Allowable Stresses
 

Internal Couple Method
Static equilibrium of internal forces
 

 

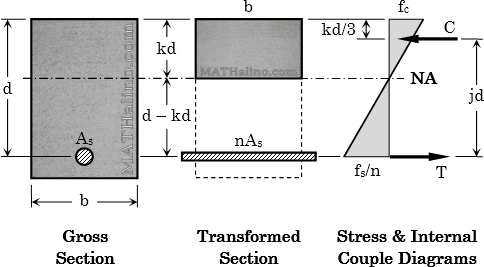
Factor k:

$k = \dfrac{f_c}{f_c + \dfrac{f_s}{n}}$

Factor j:

$j = 1 - \frac{1}{3}k$

Moment resistance coefficient:

$R = \frac{1}{2}f_c \, kj$

Moment capacity: Use the smallest of the two

$M_c = C \, jd = \frac{1}{2}f_c \, kj \, bd^2 = Rbd^2$

$M_s = T \, jd = A_s f_s \, jd$

 

Transformed Section Method
Convert steel area to equivalent concrete area by multiplying A_s with modular ratio, n.
 

 

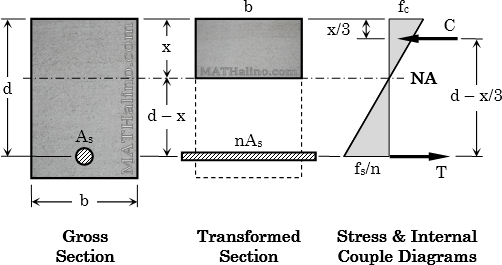
Location of the neutral axis from extreme compression fiber

Singly reinforced: $\frac{1}{2}bx^2 = nA_s(d - x)$

Doubly reinforced: $\frac{1}{2}bx^2 + (2n - 1)A_s' (x - d') = nA_s(d - x)$

 

Cracked section moment of inertia (I_NA = I_cr)

Singly reinforced: $I_{NA} = \dfrac{bx^3}{3} + nA_s(d - x)^2$

Doubly reinforced: $I_{NA} = \dfrac{bx^3}{3} + (2n - 1)A_s'(x - d')^2 + nA_s(d - x)^2$

 

Actual stresses (calculate using Flexure Formula)

Concrete
$f_c = \dfrac{Mx}{I_{NA}}$

Tension steel
$\dfrac{f_s}{n} = \dfrac{M(d - x)}{I_{NA}}$

Compression steel for doubly reinforced
$\dfrac{f_s'}{2n} = \dfrac{M(x - d')}{I_{NA}}$