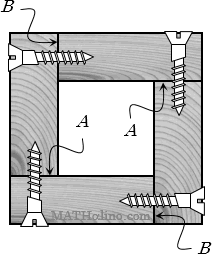
Example 01: Spacing of Screws in Box Beam made from Rectangular Wood
Problem
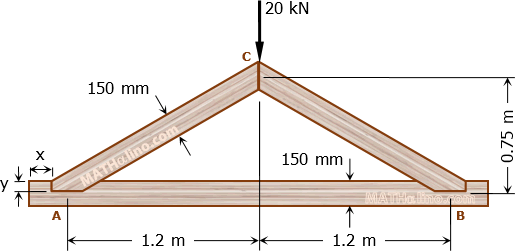
A concentrated load P is carried at midspan by a simply supported 4-m span beam. The beam is made of 40-mm by 150-mm timber screwed together, as shown. The maximum flexural stress developed is 8.3 MPa and each screw can resist 890 N of shear force.
- Determine the spacing of screws at A.
- Determine the spacing of screws at B.


Recent comments