Member JK
Equation to use: ΣMC = 0
Location of Unit Load = Point C
$U_{JK} = -\dfrac{ab}{Ld} = -\dfrac{8(8)}{16(8\sin 60^\circ)}$
$U_{JK} = -\sqrt{3}/3$
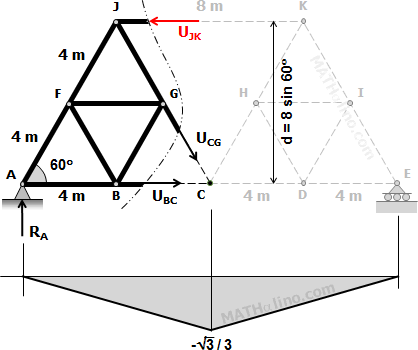Influence Diagram for Member JK
$F_{JK} = 10\left[ \frac{1}{2}(16)\left( -\sqrt{3}/3 \right) \right] + 30\left( -\sqrt{3}/3 \right)$
$F_{JK} = -63.51 ~ \text{kN}$ ← [ B ] answer for part 1
Member BC
Equation to use: ΣMJ = 0
Location of Unit Load = Point B
$U_{BC} = +\dfrac{ab}{Ld} = \dfrac{4(12)}{16(8\sin 60^\circ)}$
$U_{BC} = \sqrt{3}/4$
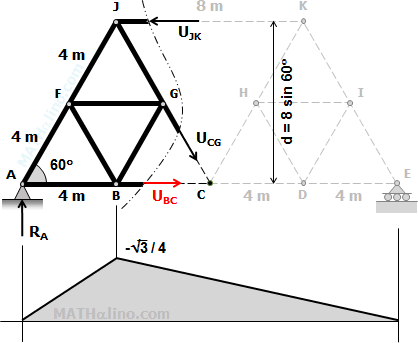Influence Diagram for Member BC
$F_{BC} = 10\left[ \frac{1}{2}(16)\left( \sqrt{3}/4 \right) \right] + 30\left( \sqrt{3}/4 \right)$
$F_{BC} = 47.63 ~ \text{kN}$ ← [ A ] answer for part 2
Member CG
Equation to use: ΣFV = 0
Location of Unit Load = Point B (Within the Section)
$U_{CGv} = -\dfrac{a}{L}$
$U_{CG}\sin 60^\circ = -\dfrac{4}{16}$
$U_{CG} = -\sqrt{3}/6$
Location of Unit Load = Point C (Outside the Section)
$U_{CGv} = +\dfrac{b}{L}$
$U_{CG}\sin 60^\circ = \dfrac{8}{16}$
$U_{CG} = \sqrt{3}/3$
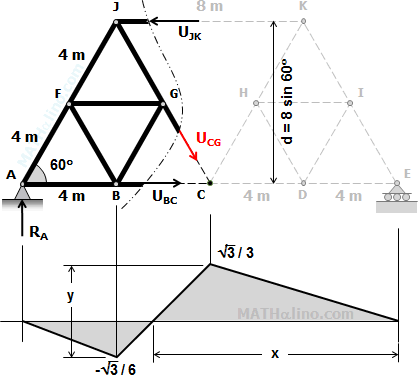Influence Diagram for Member CG
$y = \sqrt{3}/3 - \left( -\sqrt{3}/6 \right) = \sqrt{3}/2$
$\dfrac{x - 8}{\sqrt{3}/3} = \dfrac{4}{\sqrt{3}/2}$ → $x = 32/3$
Maximum Compression Force:
$F_{CG} = 10\left[ \frac{1}{2}\left(16 - \frac{32}{3} \right)\left( -\sqrt{3}/6 \right) \right] + 30\left( -\sqrt{3}/6 \right)$
$F_{CG} = -16.36 ~ \text{kN}$
Maximum Tension Force:
$F_{CG} = 10\left[ \frac{1}{2}\left(\frac{32}{3} \right)\left( \sqrt{3}/3 \right) \right] + 30\left( \sqrt{3}/3 \right)$
$F_{BC} = 47.63 ~ \text{kN}$
Answer for part 3 = [ C ]
