Structural Analysis

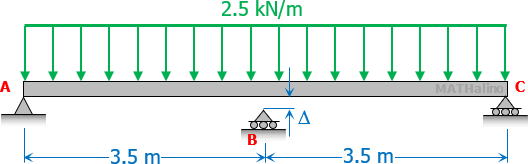
Situation
A simply supported beam has a span of 12 m. The beam carries a total uniformly distributed load of 21.5 kN/m.
1.   To prevent excessive deflection, a support is added at midspan. Calculate the resulting moment (kN·m) at the added support.

2.   Calculate the resulting maximum positive moment (kN·m) when a support is added at midspan.

3.   Calculate the reaction (kN) at the added support.

Situation
A cantilever beam, 3.5 m long, carries a concentrated load, P, at mid-length.

1.   How much is the deflection (mm) at mid-length?

2.   What force (kN) should be applied at the free end to prevent deflection?

3.   To limit the deflection at mid-length to 9.5 mm, how much force (kN) should be applied at the free end?

Situation
A simply supported steel beam spans 9 m. It carries a uniformly distributed load of 10 kN/m, beam weight already included.

1.   What is the maximum flexural stress (MPa) in the beam?

2.   To prevent excessive deflection, the beam is propped at midspan using a pipe column. Find the resulting axial stress (MPa) in the column

3.   How much is the maximum bending stress (MPa) in the propped beam?

Situation
A beam 100 mm × 150 mm carrying a uniformly distributed load of 300 N/m rests on three supports spaced 3 m apart as shown below. The length x is so calculated in order that the reactions at all supports shall be the same.
 

1.   Find x in meters.

2.   Find the moment at B in N·m.

3.   Calculate the reactions in Newton.

Situation
A beam of uniform cross section whose flexural rigidity EI = 2.8 × 10¹¹ N·mm², is placed on three supports as shown. Support B is at small gap Δ so that the moment at B is zero.
 

1.   Calculate the reaction at A.

2.   What is the reaction at B?

3.   Find the value of Δ.

Situation
The bridge truss shown in the figure is to be subjected by uniform load of 10 kN/m and a point load of 30 kN, both are moving across the bottom chord
 

Calculate the following:
1.   The maximum axial load on member JK.

2.   The maximum axial load on member BC.

3.   The maximum compression force and maximum tension force on member CG.