Influence Lines for Trusses
Example
For the Pratt truss shown below, draw the influence diagram for members JK, DK, and DE.
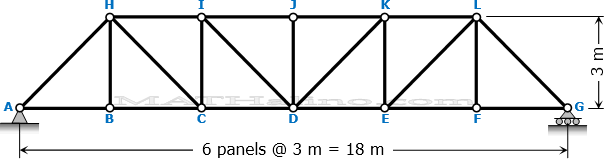
Solution
Solve for the reaction at A due to unit load that move across the bottom chord.
$\Sigma M_G = 0$
$18R_A = 1.0(18 - x)$
$R_A = 1 - \dfrac{x}{18}$
Assume forces FJK, FDE, and FDK as tension as shown in the cut section below.
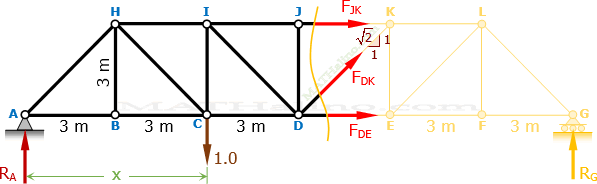
Influence Line for Member JK
For 0 ≤ x ≤ 9 m
$3F_{JK} + 9R_A = 1.0(9 - x)$
$3F_{JK} + 9\left( 1 - \dfrac{x}{18} \right) = 9 - x$
$3F_{JK} + 9 - \frac{1}{2}x = 9 - x$
$F_{JK} = -\frac{1}{6}x$ ← straight line
When x = 0, FJK = 0
When x = 9, FJK = -1.5
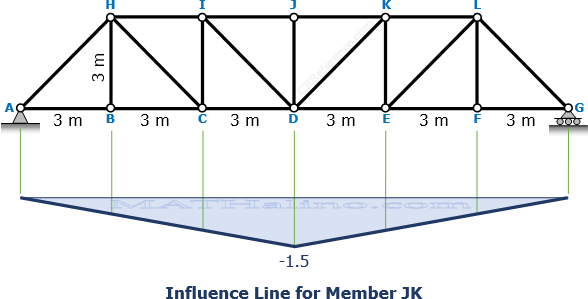
For 9 m ≤ x ≤ 18 m
$3F_{JK} + 9R_A = 0$
$3F_{JK} + 9\left( 1 - \dfrac{x}{18} \right) = 0$
$3F_{JK} + 9 - \frac{1}{2}x = 0$
$F_{JK} = \frac{1}{6}x - 3$ ← straight line
When x = 9, FJK = -1.5
When x = 18, FJK = 0
Influence Line for Member DE
For 0 ≤ x ≤ 12 m
$3F_{DE} + 1.0(12 - x) = 12R_A$
$3F_{DE} + 12 - x = 12\left( 1 - \dfrac{x}{18} \right)$
$3F_{DE} + 12 - x = 12 - \frac{2}{3}x$
$F_{DE} = \frac{1}{9}x$ ← straight line
When x = 0, FDE = 0
When x = 12, FDE = 4/3
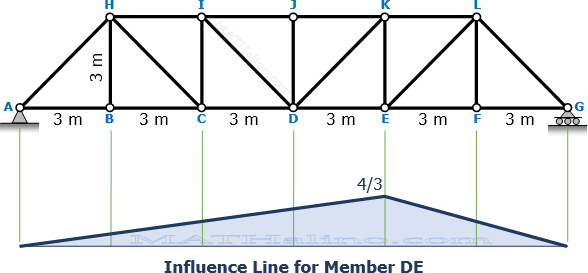
For 12 m ≤ x ≤ 18 m
$3F_{DE} = 12R_A$
$3F_{DE} = 12\left( 1 - \dfrac{x}{18} \right)$
$F_{DE} = 4 - \frac{2}{9}x$ ← straight line
When x = 12, FDE = 4/3
When x = 18, FDE = 0
Influence Line for Member DK
For 0 ≤ x ≤ 9 m
$F_{DK} \left( \frac{1}{\sqrt{2}} \right) + R_A = 1.0$
$F_{DK} \left( \frac{1}{\sqrt{2}} \right) + \left( 1 - \dfrac{x}{18} \right) = 1$
$F_{DK} = \frac{\sqrt{2}}{18}x$ ← straight line
When x = 0, FDK = 0
When x = 9, FDK = sqrt(2) / 2
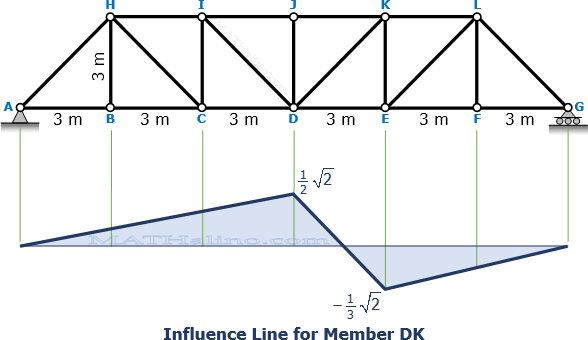
For 9 m < x ≤ 18 m
$F_{DK} \left( \frac{1}{\sqrt{2}} \right) + R_A = 0$
$F_{DK} \left( \frac{1}{\sqrt{2}} \right) + \left( 1 - \dfrac{x}{18} \right) = 0$
$F_{DK} = \frac{\sqrt{2}}{18}x - \sqrt{2}$ ← straight line
When x = 12, FDK = -sqrt(2) / 3
When x = 18, FDK = 0
